CS525 Final Project - Testing Matrix Transpose Performance in OpenCL

As a final project, we had to analyze the performance of the CUDA matrix transpose sample. I decided to work on this project using OpenCL as the reference framework.

Introduction to OpenCL

OpenCL (Open Computing Language) is an open royalty-free standard for general purpose parallel programming across CPUs, GPUs and other processors, giving software developers portable and efficient access to the power of these heterogeneous processing platforms.

OpenCL supports a wide range of applications, ranging from embedded and consumer software to HPC solutions, through a low-level, high-performance, portable abstraction. By creating an efficient, close-to-the-metal programming interface, OpenCL will form the foundation layer of a parallel computing ecosystem of platform-independent tools, middleware and applications. OpenCL is particularly suited to play an increasingly significant role in emerging interactive graphics applications that combine general parallel compute algorithms with graphics rendering pipelines.

OpenCL consists of an API for coordinating parallel computation across heterogeneous processors; and a cross-platform programming language with a well specified computation environment. The OpenCL standard:

• Supports both data- and task-based parallel programming models
• Utilizes a subset of ISO C99 with extensions for parallelism
• Defines a configuration profile for handheld and embedded devices
• Efficiently inter-operates with OpenGL, OpenGL ES and other graphics APIs

From CUDA to OpenCL

Given a CUDA program, converting it to its corresponding OpenCL implementation consists of two separate steps:

• Converting the host C/C++ code from CUDA to the OpenCL API
• Converting the CUDA kernel code to OpenCL kernels

The CUDA and OpenCL host APIs are radically different. There is no easy mapping from CUDA functionalities to OpenCL ones. For instance, while CUDA kernel calls are similar to normal function calls, OpenCL is based on a queuing mechanism. While queuing is (in my opinion) a more intuitive and consistent way to represent host / device interactions, its implementation has very little in common with CUDA. For this and other reasons, it is easier to write OpenCL code from scratch, instead of modifying an existing CUDA program.

Converting CUDA kernels

Luckily, CUDA and OpenCL kernels share a good amount of similarities, and it is possible to convert a CUDA program to OpenCL with relative ease. Here are some of the basic steps needed to perform such conversion:

1. Convert CUDA group and thread indexes into global and workgroup ids
2. Substitute __syncthread() calls into barrier(CLK_LOCAL_MEM_FENCE)
3. Move shared memory declarations to local memory kernel argument pointers
4. Convert multidimensional shared memory indexes into unidimensional array indexes for local memory

Points 1 and 2 are straightforward substitutions, while the last two steps require some additional work on the code:

Local memory (the equivalent of CUDA shared memory) cannot be declared directly inside OpenCL kernels: it has to be passed as a kernel function argument using the __local specifier. Additionally, since they are function arguments, local memory pointers need to be declared inside the host code using a clSetKernelArg call. An example of this usage can be found in the code linked at the end of this page, and in many of the OpenCL sample programs.

Since it is passed as a simple pointer, local memory cannot be indexed as a multidimensional array, as in CUDA. This means that multidimensional indexes have to be converted to unidimensional indexes. Given the following CUDA shared memory declaration:

__shared__ float tile[TILE_DIM][TILE_DIM];


A CUDA expression like tile[x][y] in OpenCL becomes tile[x * TILE_DIM + y]

OpenCL matrix transpose

For my project I decided to modify one of the standard OpenCL samples: MatrixTranspose. This example implements a single transpose kernel, implementing a simple optimization (coalesced memory access). I ported three additional CUDA kernels to OpenCL:

• The simple copy kernel - for reference.
• The naive transpose kernel - to have an example of non-optimized transpose performance
• The diagonal transpose kernel - as a reference of the 'best' CUDA kernel implementation

I also heavily modified the host code to quickly test different kernel configurations in terms of matrix size, kernel loops and block sizes. The host code has also been modified to simplify it as much as possible: most of the SDK library dependencies have been removed, along with some of the consistency checks present in the original code: The idea was to create a small, simple program that was easier to follow than the original OpenCL sample.

The program outputs its results as a comma-separated values file. This file can then be opened in excel or other similar tools to generate plots of the collected data.

Experiment setup

My initial idea was to tested the kernel performance modifying thee parameters of the original CUDA sample:

• The matrix size: I wanted to test different matrix sizes in both power-of-two size increases and constant size increases - to see how this influences partition camping
• The thread block / local memory size - to test how much bigger thread blocks influence performance
• The number of inside-kernel loop repetitions - to understand how repetitions amortize other computations inside the kernel

Sadly all of the tests were severely limited by one OpenCL issue: local workgroup sizes.

Local Workgroup Size Limitations

As CUDA, OpenCL has a limit on the local workgroup size (i.e. the number of threads in a thread block). This limit is normally set to 128 work-items (that is, threads). The major issue here is that this number appears to be limited by the actual selected kernel, and the available video card. On my machine, all of the matrix transpose were limited to a maximum of 32 threads in a local workgroup. This means that the maximum power-of-two tile size I could use was of 4 by 4 (or 5 by 5 for a non-power-of-two tile). This severely limits the amount of performance gain I could get out of shared memory usage, since all of the workgroup were handling just 4 by 4 tiles.

In turn, this severely limited the amount of testing I could perform on local memory sizes, since I could not test anything bigger than a 4 by 4 block.

I did some test with increasing local workgroup sizes (up to the 4 by 4 limit), but the only result I got was a steadily increasing performance as the local workgroup size increased. So I decided to perform all of my subsequent tests with the maximum allowed block size.

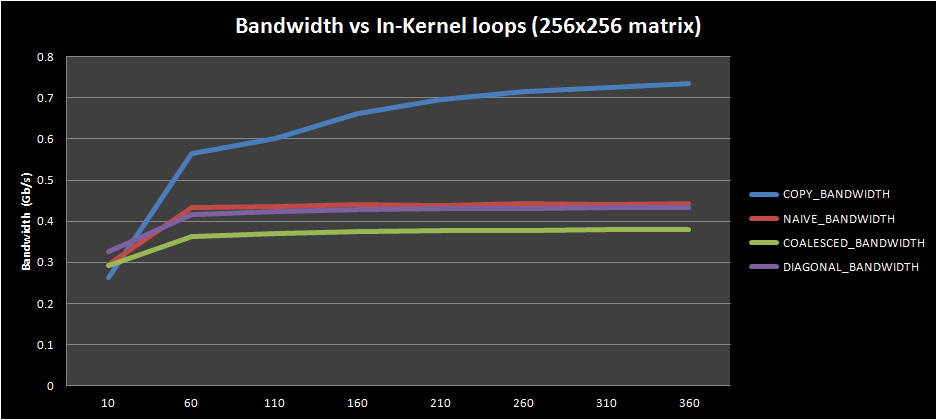
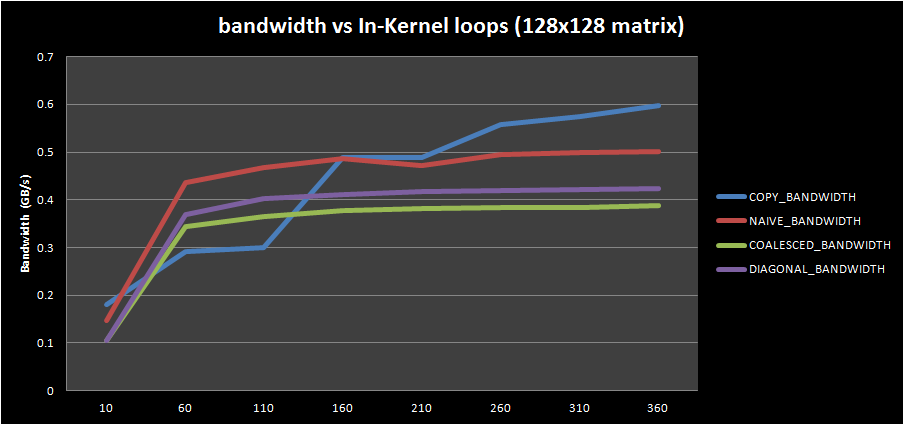
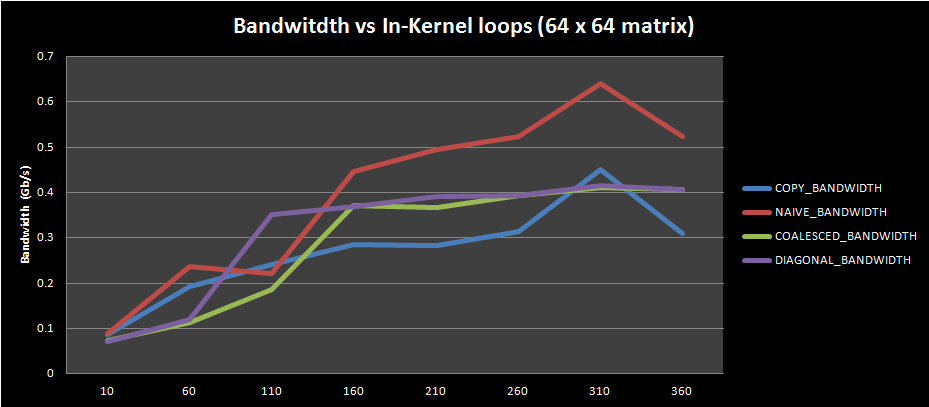
In-Kernel Loop repetitions

For this test, I changed the number of in-kernel loop repetitions for different input matrix sizes: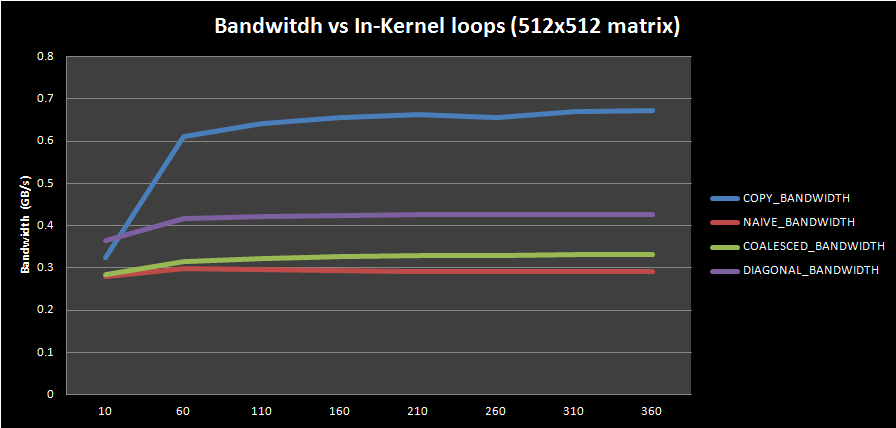 The plots for 512x512 and 256x256 matrix sizes are fairly regular: for more that 100 in-kernel repetitions the bandwidth is quite stable. The results are different for smaller matrix sizes, as in kernel loop repetitions increase, the behavior of different kernel implementations display significant variations.

Bandwidth vs Input Matrix Size

For my final test, I verified how bandwidth varied as the input matrix size changed: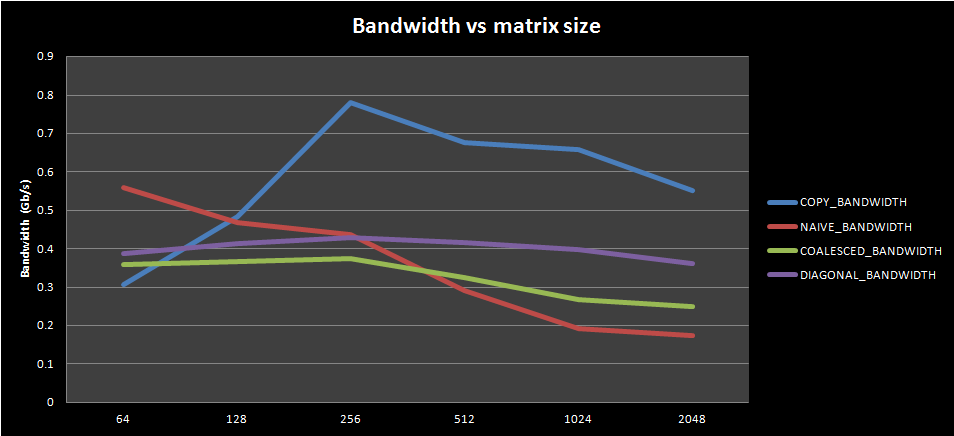

This first plot shows bandwidth change for kernels with 200 in-kernel loop repetitions (to amortize calculations for increased complexity kernels and isolate memory performance). The behavior corresponds fairly well to what is expected (copy bandwidth > diagonal transpose bandwidth > coalesced transpose bandwidth > naive transpose bandwidth), even if the bandwidth differences are different to the ones presented in the original CUDA paper. This may be due to the limited local workgroup size (as explained in the previous section) or it can be due to the different hardware present on my machine

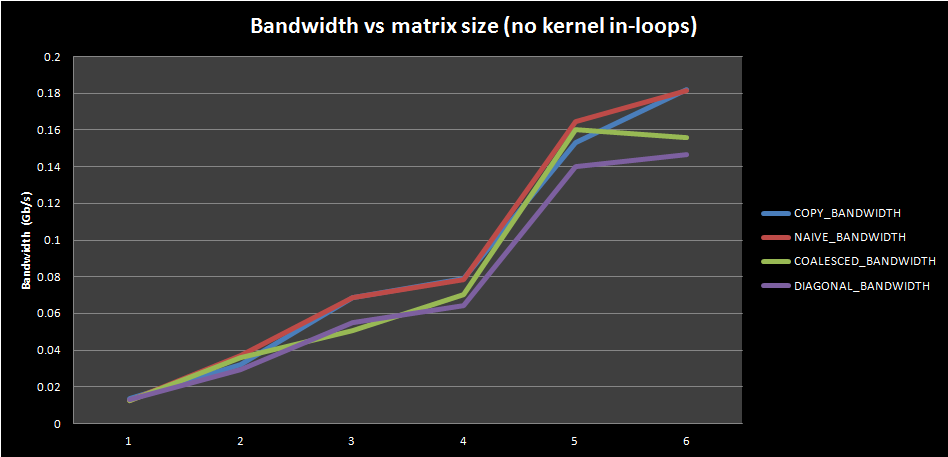
It is pretty interesting to observe the bandwidth behavior for kernels with no in-kernel loop repetitions:

For these kernels, performance follows a similar curve independently of kernel implementation: As a first look it appears that, on my specific hardware, the increased cost of index computation for more complex kernels balances the better memory performance of those kernels. But looking closer, it is possible to notice how the naive kernel and copy kernels appear to perform very similarly, which cannot be explained with index computation complexity (the two kernels are almost identical). Sadly, I was not able to pinpoint the reason of this particular result.

Downloads

>>> DOWNLOAD SOURCE CODE <<<