

Section A3.1 gives an overview of the structure of the rules component. Section A3.2 is a reference summary of the general procedure for compiling (translating) two-level rules into state transition tables. Detailed examples of how to apply the general procedure are found in sections A3.4 through A3.7. Sections A3.8 through A3.16 treat in detail various topics related to rule compilation, such as subsets, word boundary environments, complex environments, rule conflicts, and phonotactic constraints.
When the user runs PC-KIMMO and loads a set of rules from a disk file, the column headers of every state table are scanned as they are read in and a list of feasible pairs is compiled. After the rules are loaded, the user can see the entire set of feasible pairs currently in use by the rules component by issuing the list pairs command (see section 4.5.5). It should also be remembered that the set of feasible pairs is revised each time one or more rules is turned on or off by means of the set rules [ on | off ] command (see section 4.5.6.1).
Similarly, a subset name is said to stand for a set of alphabetic characters; but its effective meaning relative to a given set of rules is determined by the set of feasible pairs sanctioned by the rules. For example, in a set of rules where the subset Spal has been declared to have the members s, x, and z, the correspondence s:Spal does not represent all possible correspondences that have s as their lexical character and one of the members of the subset Spal as their surface character; rather, it represents only the feasible pairs that match its pattern, for instance s:s and s:z if these are the only correspondences involving lexical s that have been used as column headers in one or more tables. This means that using the correspondence s:Spal as a column header in a rule does not implicitly declare as feasible pairs all correspondences that match it. That is, unless the correspondence s:x is explicitly declared as a feasible pair somewhere in the set of rules, it is not included in the set of feasible pairs represented by the correspondence s:Spal. (For more on using subsets, see section A3.8.)
Each state table must be constructed such that every feasible pair is represented by one of its column headers. That is, for each table in a rule set, the entire list of feasible pairs is partitioned among the column headers with no overlap. In a table, each feasible pair belongs to one and only one column header. After loading a set of rules and compiling the list of feasible pairs, PC-KIMMO goes through the set of rules again to interpret the column headers of each table. For each table it scans the list of all the feasible pairs and assigns each one to a column header. If a feasible pair matches more than one column header, it is assigned to the most specific one, where the specificity of a column header is defined as the number of feasible pairs that match it. For example, consider a table that contains both an s:S column header and a D:P column header, where the feasible pairs that match it include t:c, d:j, and s:S. When PC-KIMMO tries to assign the feasible pair s:S to a column header in this table, it finds that it matches both the s:S column and the D:P column. PC-KIMMO will assign it to the s:S column, since it is more specific than the D:P column (one versus three pairs that match). This means that, relative to this particular rule, the D:P column header represents only two feasible pairs, namely t:c and d:j. When running PC-KIMMO, the user can see exactly how feasible pairs are assigned to the column headers of a table by using the show rule command (see section 4.5.9).
It is possible to construct a state table in which a feasible pair matches multiple column headers that have the same specificity value, thus making it impossible to uniquely assign the pair to a column header. This constitutes an incorrectly written state table. When a rules file containing such a state table is loaded, a warning message is issued alerting the user that two columns have the same specificity. If the user proceeds to analyze forms with the incorrectly written table, the pair will be assigned (arbitrarily) to the leftmost column that it matches. Correct results cannot be assured. (For more on the problem of overlapping column headers, see section A3.9.)
In order to get every feasible pair in the column headers of a table without having to literally specify each pair, a column header of the form @:@ (where @ is the ANY symbol) is included in the table. This covers all pairs that are not part of the correspondence and environment of the rule.
a. Is E the only environment in which L:S is allowed?
b. Must L always be realized as S in E?
There are four possible outcomes. Depending on the outcome, do one of the following:
a. If a is yes and b is no, posit the rule L:S => E and proceed to step 4.
b. If a is no and b is yes, posit the rule L:S <= E and proceed to step 5.
c. If both a and b are yes, posit the rule L:S <=> E and proceed to step 6.
d. If neither is yes, find the other environments in which L:S is allowed, combine these into a single disjunctive environment, and go through step 3 again.
It is also possible that it is easier to express the constraint on L:S in terms of the environment in which it is prohibited. In this case, posit the rule L:S /<= E and proceed to step 7. If L:S contains subset names, it may be necessary to write a separate table to declare as feasible pairs the correspondences that L:S is intended to represent (see sections A3.8 and A4.4).
a. Make a list of column headers for the table by writing down all the correspondences used in the expression lc L:S rc (including correspondences with @ and subset names). Add @:@ to the end of the list.
b. Beginning with state 1, add states (rows) and fill in the state transitions in the appropriate cells in the table to recognize the expression lc L:S rc. The final symbol in the expression normally should result in a transition back to state 1, except when backlooping is involved (see step 8 below).
c. Use a colon to mark state 1 as a final state (that is, 1:). Mark every state that is traversed before L:S is reached as a final state. Mark the state in which L:S is recognized as a final state. Use a period to mark all states traversed after that point as nonfinal (for instance, 2.). That is, once L:S is encountered it is not in the correct environment unless the full right context is found; thus these states cannot be final.
d. Since L:S in any other environment is not allowed, fill in the rest of the column for L:S with zeros. Furthermore, in any state traversed during the recognition of the right context, any correspondence encountered other than those provided for in rc means that L:S is in the wrong context. Thus, the rest of the cells for the states traversed in rc should be filled with zeros.
e. All remaining cells in the transition table denote successful transitions as far as this rule is concerned. In most cases, these cells are filled with transitions back to the initial state (that is, 1), except where backlooping occurs (see step 8).
a. Make a list of column headers for the table. First, put down L:S. Next, put down L:@, which now represents L:¬S. Next, write down all the correspondences used in lc and rc (including correspondences with @ and subset names). Add @:@ to the end of the list.
b. Beginning with state 1, add states (rows) and fill in the state transitions in the appropriate cells in the table to recognize the expression lc L:@ rc. The final symbol in the expression should result in failure (that is, the cell representing recognition of the final symbol should contain 0 (zero)).
c. Use a colon to mark every state as a final state.
d. All remaining cells in the transition table denote successful transitions as far as this rule is concerned. In most cases, these cells are filled with transitions back to the initial state (that is, 1), except where backlooping occurs (see step 8).
a. Make a list of column headers for the table by writing down all the correspondences used in the expression lc L:S rc (including correspondences with @ and subset names). Add @:@ to the end of the list.
b. Beginning with state 1, add states (rows) and fill in the state transitions in the appropriate cells in the table to recognize the expression lc L:S rc. The final symbol in the expression should result in failure (that is, the cell representing recognition of the final symbol should contain 0 (zero)).
c. Use a colon to mark every state as a final state.
d. All remaining cells in the transition table denote successful transitions as far as this rule is concerned. In most cases, these cells are filled with transitions back to the initial state (that is, 1), except where backlooping occurs (see step 8).
Figure A5 Semantics of two-level rules
L:S => E "Only but not always."
L is realized as S only in E.
L realized as S is not allowed in ¬E.
If L:S, then it must be in E.
Implies L:¬S in E is permitted.
L:S <= E "Always but not only."
L is always realized as S in E.
L realized as ¬S is not allowed in E.
If L is in E, then it must be L:S.
Implies L:S may occur elsewhere.
L:S <=> E "Always and only."
L is realized as S only and always in E.
Both L:S => E and L:S <= E.
Implies L:S is obligatory in E and occurs nowhere else.
L:S /<= E "Never."
L is never realized as S in E.
L realized as S is not allowed in E.
If L is in E, then it must be L:¬S.
Figure A6 Truth tables for two-level rules+---------------------------------------------------------------------------------+ | There is an L. || Is the rule satisfied? | |-----------------------------++--------------------------------------------------| | Is it realized | Is it in || | | | | | as S? | E? || L:S => E | L:S <= E | L:S <=> E | L:S /<= E | |-----------------+-----------++-----------+-----------+-------------+------------| | T | T || T | T | T | F | | T | F || F | T | F | T | | F | T || T | F | F | T | | F | F || T | T | T | T | +---------------------------------------------------------------------------------+
LR: ap+ma ap+ma ap+ba SR: ab0ma ap0ma ap0baAccording to the diagnostic questions in part 3, these correspondences indicate that p is not always realized as b before +m (p:p also occurs before +m), but that +m is the only environment in which p:b is allowed. Therefore, posit a => rule:
R35 p:b => ___ +:0 mTo compile rule R35 to a state table, follow the steps in part 4. First (step 4a), make a list of the column headers, consisting of all the correspondences used in rule R35 plus @:@:
p + m @
b 0 m @
The order of the columns of a state table do not affect its operation,
but it is helpful to the reader to keep the columns in the same order
as lc L:S rc so far as possible.
Next (step 4b), add rows (representing states) and fill in the cells with transitions to recognize the sequence p:b +:0 m:m. When the final symbol of the sequence (m:m) is reached, a transition is made back to state 1.
p + m @
b 0 m @
-------
1 2
2 3
3 1
Next (step 4c), mark state 1 as a final state (that is, 1:). This allows
the table to succeed on any correspondence that does not occur in
L:S rc. Step 4c says that every state traversed before and
including the state where L:S is recognized is marked as a
final state. Since p:b is recognized in state 1, this is
irrelevant. However, all states traversed after that point must be
marked as nonfinal; that is, once p:b is recognized, it is
not in the correct environment until the entire right context is found.
Thus, states 2 and 3 cannot be final.
p + m @
b 0 m @
-------
1: 2
2. 3
3. 1
Next (step 4d), fill in the rest of the column for p:b with
zeros, since p:b in any other environment is not allowed.
Also, for all the states traversed during the recognition of the right
context, any correspondences other than those that are part of the
right context mean that p:b is in the wrong context. Thus,
the rest of the cells in rows 2 and 3 must be filled with zeros:
p + m @
b 0 m @
-------
1: 2
2. 0 3 0 0
3. 0 0 1 0
Finally (step 4e), all remaining cells are successful transitions for
this rule and can be filled in with transitions back to the initial
state (that is, state 1). Note that since the remaining empty cells are
in state 1 and do not involve the first correspondence of L:S
rc, backlooping (part 8) is not involved. Table T35 now gives the complete transition table for rule R35.
T35 => table with right context
p + m @
b 0 m @
-------
1: 2 1 1 1
2. 0 3 0 0
3. 0 0 1 0
LR: ap+ma ap+ba ap+ba SR: ab0ma ap0ba ab0baAccording to the questions in part 3, these correspondences indicate that p is always realized as b before +m, but +m is not the only environment in which p:b is allowed (p:b also occurs before +b). Therefore, posit a <= rule:
R36 p:b <= ___ +:0 mTo compile rule R36 to a state table, follow the steps in part 5. First (step 5a), make a list of the column headers, consisting of p:b, p:@, the correspondences used in the right context, and @:@:
p p + m @
b @ 0 m @
Due to the presence of p:b, p:@ means all
other feasible pairs with a lexical p. In other words, it
represents p:¬b.
Next (step 5b), add rows (states) and fill in the cells with transitions to recognize the sequence p:@ +:0 m:m. When the final symbol of the sequence is reached (m:m), the cell is filled with zero, indicating failure.
p p + m @
b @ 0 m @
---------
1 2
2 3
3 0
Next (step 5c), mark every state as final:
p p + m @
b @ 0 m @
---------
1: 2
2: 3
3: 0
Finally (step 5d), all remaining cells denote successful transitions
back to the initial state and are filled in with ones, with the
exception of cells where backlooping applies. To demonstrate
backlooping, we will first ignore it and fill in the table with ones:
T36 p p + m @
b @ 0 m @
---------
1: 1 2 1 1 1
2: 1 1 3 1 1
3: 1 1 1 0 1
There is a problem with this state table. As written, table T36 does not work correctly with more than one
p in succession. For instance, given the lexical form
app+ma, it will return appma, without voicing
the second p. Step the example app+ma through
table T36 to verify this. When the second
p:p is encountered while in state 2, the FST will make a
transition back to state 1, where +:0 and m:m
are recognized, leaving the FST in state 1. To remedy this, the FST
must loop back to state 2 when it encounters p:p:
T36a p p + m @
b @ 0 m @
---------
1: 1 2 1 1 1
2: 1 2 3 1 1
3: 1 1 1 0 1
But table T36a will still fail to recognize an input
form such as ap+p+ma. This is because when the second
p:p is encountered in state 3, the FST will make a
transition back to state 1, again losing the fact that we are in the
environment for the change. The table must be revised so that the FST
will loop back to state 2 when a p:p is encountered in
state 3 as well:
T36b <= table with right context
p p + m @
b @ 0 m @
---------
1: 1 2 1 1 1
2: 1 2 3 1 1
3: 1 2 1 0 1
This is an example of the explanation given in part 8 of how to handle
backlooping. Backlooping is a subtle but important point, and is the
source of many errors in compiling tables. The name is intended to
convey the idea that the FST must have transitions (loops) back to the
states where symbols (or sequences of symbols) of the expression
lc L:S rc have been recognized. The notion of backlooping
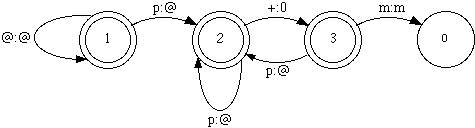
transitions is clearer when the FST is represented as a diagram; see
figure A7 (which is equivalent to table
T36b, except that transitions back to state 1 are
not drawn). There are two backloops in this FST: from state 2 there is
an arc for p:@ back to state 2, and from state 3 there is
another arc for p:@ back to state 2.
Figure A7 FST with backlooping

Why didn't we encounter backlooping while writing the state table for rule R35 above? With respect to backlooping, it may seem that table T35 should be written as follows (where states 2 and 3 have an arc back to state 2 if a p:b is recognized):
T35a p + m @
b 0 m @
-------
1: 2 1 1 1
2. 2 3 0 0
3. 2 0 1 0
The answer is that in this case step 4d overrides backlooping. Rule R35 is a => rule, which means that the correspondence
p:b is disallowed in any environment other than preceding
+m. Table T35a, however, would allow
p:b to occur preceding another p:b or
preceding the sequence +:0 p:b. To prevent this, step 4d
requires the p:b column to contain zeros in states 2 and
3.
As a matter of practice in writing a state table, the analyst should carefully check the column that represents the first symbol of the expression lc L:S rc to see which state to loop back to in each state of the table.
Often it does not seem necessary in practice to account for backlooping because of language-specific phonotactic constraints. Taking the example word app+ma discussed above, suppose that the language being described does not have morphemes like app; that is, a phonotactic constraint prohibits the sequence VCC. In such a case, state table T36 (written without backloops) would always work correctly as long as it was given input conforming to the phonotactic constraints of the language. There are two reasons why we recommend that the user of PC-KIMMO write tables that account for backlooping even when it seems unnecessary.
First, if you are inductively developing a phonological analysis, you will not necessarily know all the phonotactic constraints until the entire analysis is completed. If rules are written with incorrect backloops, puzzling failures may occur when further data are collected that contain new phonotactic patterns.
Second, it is conceptually cleaner to keep phonotactic constraints separate from the general phonological rules. Rather than incorporating phonotactic constraints in tables that encode phonological rules, it is better to write tables so that they are minimally restrictive with respect to phonotactics. The analyst can encode phonotactic constraints in a set of rules (tables) dedicated specifically to that purpose. For more discussion on expressing phonotactic constraints, see section A3.16.
LR: ap+ma ap+ba SR: ab0ma ap0baAccording to the questions in part 3, these correspondences indicate that p is always realized as b before +m, and that +m is the only environment in which p:b is allowed. Therefore, posit a <=> rule:
R37 p:b <=> ___ +:0 mAs was explained in part 6 of section A32., a <=> rule can be compiled as two separate state tables, one for the <= rule and one for the => rule. This is what has been done to produce state tables T35 and T36b above. Alternatively, a <=> rule can be compiled as a single table. To do this (see part 6), first construct the column headers by following the instructions in step 5a:
p p + m @
b @ 0 m @
Next perform steps 5b through 5d to construct the <= part of the
rule:
p p + m @
b @ 0 m @
---------
1: 2 1 1 1
2: 2 3 1 1
3: 2 1 0 1
Now perform steps 4b through 4e to add the => part of the rule:
T37 <=> table with right context
p p + m @
b @ 0 m @
---------
1: 4 2 1 1 1
2: 4 2 3 1 1
3: 4 2 1 0 1
4. 0 0 5 0 0
5. 0 0 0 1 0
Notice that to recognize p:b and the right context
+:0 m:m, two states (4 and 5, corresponding to states 2
and 3 in table T35) must be added to the table. These
states are nonfinal states.
Special attention must be paid to the transitions in states 2 and 3 of table T37. For the p:@ column, states 2 and 3 must loop back to state 2, which is the state in the <= part of the rule where p:@, the first symbol of the expression lc L:S rc, has been recognized. This is identical to table T36b. For the p:b column, states 2 and 3 must make a transition to state 4, which is the second state of the => part of the rule. This is the same transition as in state 1.
R38 p:b /<= ___ +:0 mThe state table that encodes rule R38 must recognize the sequence p:b +:0 m:m and then forbid it. As the left arrow of the /<= operator suggests, the semantics of this rule type is most similar to the <= rule. Whereas rule R36 above (a <= rule) states that p is always (obligatorily) realized as b before +:0 m but may also be realized as b in some other environment, rule R38 (a /<= rule) states that p is always (obligatorily) prohibited before +:0 m:m, but may be realized as b in some other environment.
To compile rule R38 to a state table, follow the steps in part 7. First (step 7a), make a list of the column headers needed to recognize p:b and the environment plus @:@:
p + m @
b 0 m @
Notice that unlike table T36b, which expresses a
<= rule, we do not need a p:@ column header. This is
because table T36b is built to prohibit the sequence
p:¬b +:0 m:m, but the table we are building for a
/<= rule must prohibit p:b +:0 m:m.
Next (step 7b), add rows (states) and fill in the cells with transitions to recognize the sequence p:b +:0 m:m. When the final symbol of the sequence is reached (m:m), the cell is filled with zero, indicating failure.
p + m @
b 0 m @
-------
1 2
2 3
3 0
Next (step 7c), mark every state as final:
p + m @
b 0 m @
-------
1: 2
2: 3
3: 0
Finally (step 7d), all remaining cells denote successful transitions and
are filled in with ones, with the exception of cells that meet the
conditions of backlooping (part 8). Specifically, the cells in column
p:b for states 2 and 3 must make a transition back to
state 2, since state 2 represents the state where the first symbol
(p:b) of the expression lc L:S rc has been
recognized.
T38 /<= table with right context
p + m @
b 0 m @
-------
1: 2 1 1 1
2: 2 3 1 1
3: 2 1 0 1
It is instructive to compare table T38 with both
table T35 (for a => rule) and table T36b (for a <= rule).
LR: am+pa am+pa ab+pa SR: am0ba am0pa ab0paAccording to the diagnostic questions in part 3, these correspondences indicate that p is not always realized as b after m+ (p:p also occurs after m+), but that m+ is the only environment in which p:b is allowed. Therefore posit a => rule:
R39 p:b => m +:0 ___To compile rule R39, first (step 4a) make a list of the column headers:
m + p @
m 0 b @
Next (step 4b), add rows and fill in the cells to recognize the sequence
m:m +:0 p:b:
m + p @
m 0 b @
-------
1 2
2 3
3 1
Next (step 4c), mark state 1 as a final state. Also, every state
traversed up to and including the state where p:b is
recognized is marked as a final state. Since there is no right context,
there are no more states after that point.
m + p @
m 0 b @
-------
1: 2
2: 3
3: 1
Next (step 4d) fill in the rest of the p:b column with
zeros, because the p:b correspondence cannot succeed until
the entire left context has been recognized:
m + p @
m 0 b @
-------
1: 2 0
2: 3 0
3: 1
Finally (step 4e), all remaining cells are successful transitions for
this rule and can be filled in with transitions back to the initial
state (state 1), with the exception of cells that meet the conditions
of backlooping (part 8). Specifically, the cells in column
m:m for states 2 and 3 must make a transition back to
state 2, since state 2 represents the state where the first symbol
(m:m) of the expression lc L:S rc has been
recognized. Now table T39 will work correctly with
input forms such as amm+pa and am+m+pa.
T39 => table with left context
m + p @
m 0 b @
-------
1: 2 1 0 1
2: 2 3 0 1
3: 2 1 1 1
LR: am+pa ab+pa ab+pa SR: am0ba ab0pa ab0baAccording to the questions in part 3, these correspondences indicate that p is always realized as b after m+, but m+ is not the only environment in which p:b is allowed (it also occurs after b+). Therefore, posit a <= rule:
R40 p:b <= m +:0 ___To compile rule R40, first (step 4a) make a list of the column headers, including p:@:
m + p p @
m 0 b @ @
Due to the presence of p:b, p:@ means all
other feasible pairs with a lexical p. In other words, it
represents p:¬b.
Next (step 5b), add rows and fill in the cells to recognize the sequence m:m +:0 p:@. When the final symbol of the sequence is reached (p:@), the cell is filled with zero, indicating failure.
m + p p @
m 0 b @ @
---------
1 2
2 3
3 0
Next (step 5c), mark every state as final:
m + p p @
m 0 b @ @
---------
1: 2
2: 3
3: 0
Finally (step 5d), all remaining cells are successful transitions for
this rule, and can be filled in with transitions back to the initial
state (state 1), with the exception of cells that meet the conditions
of backlooping (part 8). Specifically, the cells in column
m:m for states 2 and 3 must make a transition back to
state 2, since state 2 represents the state where the first symbol
(m:m) of the expression lc L:S rc has been
recognized. Now table 4 will work correctly with input forms such as
amm+pa and am+m+pa.
T40 <= table with left context
m + p p @
m 0 b @ @
---------
1: 2 1 1 1 1
2: 2 3 1 1 1
3: 2 1 1 0 1
LR: am+pa ab+pa SR: am0ba ab0paAccording to the questions in part 3, these correspondences indicate that p is always realized as b after m+, and m+ is the only environment in which p:b is allowed. Therefore, posit a <=> rule:
R41 p:b <=> m +:0 ___As is explained in part 6 of section A3.2, a <=> rule can be compiled as two separate state tables, one for the <= rule and one for the => rule. This is what has been done to produce state tables T39 and T40 above. Alternatively, a <=> rule can be compiled as a single table. To do this (see part 6), first construct the column headers following the instructions in step 5a:
m + p p @
m 0 b @ @
Next perform steps 5b through 5d to construct the <= part of the
rule:
m + p p @
m 0 b @ @
---------
1: 2 1 1 1
2: 2 3 1 1
3: 2 1 0 1
Now perform steps 4b through 4e to add the => part of the rule. Since
rule R41 has no right context, no new states need to
be added. Simply fill in the column for p:b. Notice that
in states 1 and 2 the p:b column must be filled with zeros
just as it is in rule R39. If we encounter
p:@ in state 3, then we fail; if we encounter
p:b, then we succeed.
T41 <=> table with left context
m + p p @
m 0 b @ @
---------
1: 2 1 0 1 1
2: 2 3 0 1 1
3: 2 1 1 0 1
R42 p:b /<= m +:0 ___To compile rule R42 to a state table, follow the steps in part 7. First (step 7a), make a list of the column headers needed to recognize p:b and the environment plus @:@:
m + p @
m 0 b @
Next (step 7b), add rows (states) and fill in the cells with transitions
to recognize the sequence m:m +:0 p:b. When the final
symbol of the sequence is reached (p:b), the cell is
filled with zero, indicating failure.
m + p @
m 0 b @
-------
1 2
2 3
3 0
Next (step 7c), mark every state as final:
m + p @
m 0 b @
-------
1: 2
2: 3
3: 0
Finally (step 7d), all remaining cells denote successful transitions and
are filled in with ones with the exception of cells that meet the
conditions of backlooping (part 8). Specifically, the cells in column
m:m for states 2 and 3 must make a transition back to
state 2, since state 2 represents the state where the first symbol
(m:m) of the expression lc L:S rc has been
recognized.
T42 /<= table with left context
m + p @
m 0 b @
-------
1: 2 1 1 1
2: 2 3 1 1
3: 2 1 0 1
LR: sasa sasa SR: saza sasaAccording to the diagnostic questions in part 3, these correspondences indicate that s is not always realized as z between vowels (s:s also occurs between vowels), but that between vowels is the only environment in which s:z is allowed. Therefore, posit a => rule:
R43 s:z => V ___ VTo compile rule R43 to a state table, follow the steps in part 4:
T43 => table with left and right contexts
V s @
V z @
-----
1: 2 0 1
2: 2 3 1
3. 2 0 0
While rule R43 contains the correspondence
V:V twice, table T43 has only one
V:V column header. The single V:V header
serves for both instances of the correspondence in the environment.
Having two identical column headers in a table will result in an error.
(See also section A3.8 on using subsets in
state tables.)
Notice that states 1 and 2 are final, while state 3 is nonfinal. Also note carefully that accounting for backlooping requires the transition in state 2 in the V:V column to remain in state 2. This is necessary to allow the correct recognition of words with consecutive vowels, for instance saasa. Less obvious is that when V:V is recognized in state 3 the FST must return to state 2 rather than the expected state 1. This is necessary to allow the rule to apply more than once in the same word where the environments overlap. For example, consider these forms:
LR: asasa SR: azazaIn this example, the second a serves both as the right context of the first s:z correspondence and as the left context of the second s:z correspondence. Therefore, when it is first recognized in state 3 of the table, a transition must be made back to state 2 so that the rule can apply again.
LR: sasa sasa SR: saza zazaAccording to the questions in part 3, these correspondences indicate that s is always realized as z between vowels, but between vowels is not the only environment in which s:z is allowed (it also occurs word-initially). Therefore, posit a <= rule:
R44 s:z <= V ___ VTo compile rule R44, follow the steps in part 5:
T44 <= table with left and right contexts
V s s @
V z @ @
-------
1: 2 1 1 1
2: 2 1 3 1
3: 0 1 1 1
To account for backlooping, state 2 must have a 2 in the
V:V column, parallel to table T43. But
unlike table T43, state 3 must have a 0 in the
V:V column, not a 2. This is because rule R44 is a <= rule and must disallow the sequence
V:V s:@ V:V. However, table T44 still
correctly handles lexical forms such as asasa because only
states 1 and 2 are used.
LR: sasa SR: sazaAccording to the questions in part 3, these correspondences indicate that s is always realized as z between vowels, and between vowels is the only environment in which s:z is allowed. Therefore, posit a <=> rule:
R45 s:z <=> V ___ VTo compile rule R45, follow the steps in part 6:
T45 <=> table with left and right contexts
V s s @
V z @ @
-------
1: 2 0 1 1
2: 2 4 3 1
3: 0 0 1 1
4. 2 0 0 0
Rows 1 through 3 constitute the <= part of the rule (compare rule R44), and rows 1, 2, and 4 constitute the => part of
the rule (compare rule R43).
R46 s:z /<= V ___ VTo compile rule R46 to a state table, follow the steps in part 7:
T46 /<= table with left and right contexts
V s @
V z @
-----
1: 2 1 1
2: 2 3 1
3: 0 1 1
ROOT ROOT+i
---- ------
?unum `six' ?unumi `make it six'
?usa `one' ?usahi `make it one'
In the following two-level representations, the inserted h
is represented as corresponding to a lexical NULL symbol (zero):
LR: ?unum+i ?usa+0i SR: ?unum0i ?usa0hiThe => rule for h-insertion is written as expected:
R47 h-insertion
0:h => V +:0 ___ V
and is compiled into a state table in the usual way:
T47 h-insertion
V + 0 @
V 0 h @
-------
1: 2 1 0 1
2: 2 3 0 1
3: 2 1 4 1
4. 2 0 0 0
Constructing the <= table, however, is not as straightforward.
Following the general procedure for compiling <= rules to tables, we
might expect to construct a the <= table using the column headers
0:h and 0:@, where 0:@ is
intended to specify 0:¬h (that is, a lexical
0 corresponding to anything except a surface
h):
R48 h-insertion
0:h <= V +:0 ___ V
T48 h-insertion
V + 0 0 @
V 0 h @ @
---------
1: 2 1 1 1 1
2: 2 3 1 1 1
3: 2 1 1 4 1
4: 0 1 1 1 1
Unfortunately, if we submit the lexical input form
?usa+i to rules R47 and R48, both the correct result
?usahi and the incorrect result
?usai will be returned. Why didn't rule R48, the <= rule, force the insertion of
h as expected? The answer is in the meaning of the column
header 0:@. What we really want the <= rule to do is to
recognize the absence of an inserted h in the specified
environment and then to fail, that is, to prohibit the sequence V
+:0 V. In effect this means that the table would have to
recognize the correspondence 0:0 as an instance of the
column header 0:@. However, 0:0 is not a
feasible pair (and indeed never could be); thus the column header
0:@ cannot specify 0:0. As a matter of fact,
if there are no other insertion correspondences in the description,
PC-KIMMO will report an error when it tries to interpret table T48, since there would be no feasible pairs that
would match the 0:@ column header.
The answer to writing a table that makes h-insertion obligatory (that is, the effect of a <= rule) is that it is necessary only to disallow the sequence V +:0 V. This can be easily done with a /<= rule of this form:
R49 h-insertion
0:0 /<= V +:0 ___ V
This rule must be understood in a special way. Although it follows the
general syntax of two-level rules (correspondence, operator,
environment), it departs from the normal meaning of two-level rules in
that its correspondence part, namely 0:0, is not a
feasible pair. However, its intended meaning is clear when it is
compared to the corresponding => rule (see the rule in the header
line in table T47). It simply means that something
must be inserted where the environment line is located. The => rule
provides the h, which is inserted at this point. The table
that expresses rule R49 looks like this:
T49 h-insertion
V + @
V 0 @
-----
1: 2 1 1
2: 2 3 1
3: 0 1 1
Now it is obvious that the two rules can be combined as a single <=> rule.
R50 h-insertion
0:h <=> V +:0 ___ V
T50 h-insertion
V + 0 @
V 0 h @
-------
1: 2 1 0 1
2: 2 3 0 1
3: 0 1 4 1
4. 2 0 0 0
SUBSET D t d s SUBSET P c j S SUBSET Vhf i eIn section A1.4 a rule using these subsets was introduced, repeated here as rule R51.
R51 Palatalization
D:P => ___ Vhf
Rule R51 states that the alveolar consonants in subset
D may be realized as the palatalized consonants in subset
P when they occur preceding the high, front vowels in
subset Vhf. Specifically, we want the subset
correspondence D:P to stand for the feasible pairs
t:c, d:j, and s:S.
Translating rule R51 into a state table is
straightforward:
T51 Palatalization
D Vhf @
P Vhf @
-------
1: 2 1 1
2. 0 1 0
However, a two-level description containing table T51
will produce no correct results unless the feasible pairs
t:c, d:j, and s:S are
declared explicitly. The pairs must appear as column headers in a table
somewhere in the description. This is typically done by constructing a
table specifically for the purpose of declaring special
correspondences. For example, the following table declares the feasible
pairs that we want for the column header D:P:
T52 Palatalization correspondences
t d s @
c j S @
-------
1: 1 1 1 1
Now the D:P column header in table T51
will recognize all and only the pairs declared in table T52. Similarly, the feasible pairs that
Vhf:Vhf stands for (that is, i:i and
e:e) must be declared somewhere in the description. Since
in this case the pairs are default correspondences, they will typically
be included in the table with all the other default correspondences.
R53 t:c => V ___ iA first attempt at writing a state table for rule R53 might look like this:
T53 V t i @
V c i @
-------
1: 2 0 1 1
2: 2 3 1 1
3. 0 0 1 0
Given the lexical form mati, table T53
will correctly produce the surface form maci. But given
the form miti, it will fail to produce the expected result
mici. This is because of the interaction of the column
headers V:V and i:i. Because the feasible
pair i:i is an instance of V:V, we might
expect that the first i in the input form
miti would match the V:V column header and
cause a successful transition to state 2. This is not the case. For
each table in a PC-KIMMO description, the entire set of feasible pairs
must be partitioned among the column headers with no overlap. Each
feasible pair belongs to one and only one column header. When PC-KIMMO
interprets the column headers of a table, it scans the list of all the
feasible pairs and assigns each one to a column header. If a feasible
pair matches more than one column header, it assigns it to the most
specific one, where the specificity of a column header is defined as
the number of feasible pairs that matches it. In order to see exactly
how the feasible pairs are assigned to the column headers of a rule,
use the show rule command (see section 4.5.9).
Thus in table T53 the feasible pair i:i potentially matches both the column headers V:V and i:i; but because i:i is more specific than V:V, the pair i:i is assigned to the column header i:i. This means that the column header V:V stands for all the feasible pairs of vowels except i:i. Thus the input pair i:i matches only the column header i:i. To work correctly, table T53 must allow i:i to be an instance of V:V in the left context by placing a 2 in states 1 and 2 under the i:i header. Note also that the order of the columns has no effect on which column header an input pair is matched to. Table T53a reflects these changes.
T53a V t i @
V c i @
-------
1: 2 0 2 1
2: 2 3 2 1
3. 0 0 2 0
Now consider a description that contains a subset Vrd for
rounded vowels and a subset Vhi for high vowels:
SUBSET Vrd o u SUBSET Vhi i e o uNotice that the Vhi subset properly includes the Vrd subset. Assume that the description contains the following rule:
R54 t:c => Vrd ___ VhiWe first write a state table for rule R54 like this:
T54 Vrd t Vhi @
Vrd c Vhi @
-----------
1: 2 0 1 1
2: 2 3 1 1
3. 0 0 1 0
But the feasible pairs o:o and u:u, which
match both the Vrd:Vrd and Vhi:Vhi column
headers, must belong to the Vrd:Vrd column, since it is
more specific. Thus the Vhi column represents only the
pairs i:i and e:e. This means that a lexical
input form such as utu will not produce the expected
surface form ucu, because the second u will
always match Vrd, not Vhi. This problem is
fixed by including u:u and o:o as column
headers in table T54a:
T54a Vrd t Vhi u o @
Vrd c Vhi u o @
---------------
1: 2 0 1 2 2 1
2: 2 3 1 2 2 1
3. 0 0 1 2 2 0
The solution, then, in cases of overlapping column headers is to
explicitly include as headers in the table the feasible pairs that
belong to both headers.
It is possible to construct a state table in which a feasible pair matches multiple column headers that have the same specificity value, making it impossible to uniquely assign the pair to a column. This constitutes an incorrectly written state table. When the rules file containing such a state table is loaded, a warning message is issued alerting the user that two columns have the same specificity. If the user proceeds to analyze forms with the incorrectly written table, a pair will be assigned (arbitrarily) to the leftmost column that it matches. Correct results cannot be assured.
LR: mabab SR: mabapAssume these subsets for voiced stops (B) and voiceless stops (P):
SUBSET B b d g SUBSET P p t kTwo-level rules use the BOUNDARY symbol (#) to indicate word boundary:
R55 Devoicing
B:P <=> ___ #
The corresponding state table is written with #:# as the
column header representing word boundary. Note that a boundary symbol
used in a column header can only correspond to another boundary symbol;
that is, correspondences such as #:0 are illegal.
T55 Devoicing
B B # @
P @ # @
-------
1: 3 2 1 1
2: 3 2 0 1
3. 0 0 1 0
Rules and tables that refer to an initial word boundary are written in a
similar way. Here is a rule for word-initial spirantization.
R56 Spirantization
p:f <=> # ___ V
T56 Spirantization
# p p V @
# f @ V @
---------
1: 2 0 1 1 1
2: 1 4 3 1 1
3: 1 0 1 0 1
4. 0 0 0 1 0
(Notice that since the first symbol of lc L:S rc is initial
word boundary, backlooping is irrelevant.)
As an example we will use a vowel reduction rule. It states that a vowel followed by some number of consonants followed by stress (indicated by ') is reduced to schwa (ê). For example,
LR: bab'a bamb'a SR: bêb'a bêmb'aIn rule R57 we treat the case where there is exactly one or two intervening consonants. Parentheses indicate that the second consonant is optional.
R57 V:ê => ___ C(C)'In table T57, the second, optional consonant is implemented in state 3. The table succeeds when it recognizes the stress, either in state 3 after finding one consonant, or in state 4 after finding another consonant.
T57 Vowel Reduction
V C ' @
ê C ' @
-------
1: 2 1 1 1
2. 0 3 0 0
3. 0 4 1 0
4. 0 0 1 0
Rule R58 and table T58 specify
either zero, one, or two consonants.
R58 Vowel Reduction
V:ê => ___ (C)(C)'
T58 Vowel Reduction
V C ' @
ê C ' @
-------
1: 2 1 1 1
2. 0 3 1 0
3. 0 4 1 0
4. 0 0 1 0
The only difference from table T57 is found in state 2
of table T58, where it is allowed to encounter the
stress immediately after the V:ê correspondence.
In rule R59 the asterisk indicates zero or more instances of C.
R59 Vowel Reduction
V:ê => ___ C*'
Table T59 succeeds in state 2 either by immediately
finding stress or by repeating state 2 to find consonants until stress
is reached.
T59 Vowel Reduction
V C ' @
ê C ' @
-------
1: 2 1 1 1
2. 0 2 1 0
Rule R60 specifies one or more consonants.
R60 Vowel Reduction
V:ê => ___ CC*'
R60 Vowel Reduction
V C ' @
ê C ' @
-------
1: 2 1 1 1
2. 0 3 0 0
3. 0 3 1 0
Here state 2 requires that at least one consonant be found. Then state 3
functions like state 2 of the previous example to repeat consonants
until stress is found.
Section A1.6 discussed multiple environments in two-level rules. In this section the state tables for those rules are provided. The example used here is a vowel lengthening rule. It states that the correspondence a:ä (short and long a) occurs in two distinct environments: when it is stressed (tonic lengthening) or when it occurs in the syllable preceding stress (pretonic lengthening). For example,
LR: ladab'ar SR: ladäb'ärFirst, the tonic and pretonic lengthening rules and tables are written as separate rules:
R61 Pretonic Lengthening
a:ä => ___ C'
T61 Pretonic Lengthening
a C ' @
ä C ' @
-------
1: 2 1 1 1
2. 0 3 0 0
3. 0 0 1 0
R62 Tonic Lengthening
a:ä => ' ___
T62 Tonic Lengthening
' a @
' ä @
-----
1: 2 0 1
2: 2 1 1
Note that in state 2 the 2 under the stress header is due to
backlooping, even though we do not expect to have two stress marks in
succession (see section A3.4).
As discussed in section A1.6, rules R61 and R62 are contradictory; they both claim to specify the only environment in which a:ä is allowed. They must be combined into a single rule, rule R63, which is expressed as state table T63.
R63 Pretonic and Tonic Lengthening
a:ä => [ ___ C'| ' ___ ]
T63 Pretonic and Tonic Lengthening
a C ' @
ä C ' @
-------
1: 2 1 4 1
2. 0 3 0 0
3. 0 0 4 0
4: 1 1 4 1
There is one key difference between table T63, and
tables T61 and T62. This is the
change in state 3 where stress now makes a transition to state 4 rather
than back to state 1. This is necessary because stress (which is in the
right context of rule R61) is the first symbol of the
left context of rule R62. (Note that in state 4 in
the stress column the transition back to state 4 is due to
backlooping.)
Rules R64 and R65 and tables T64 and T65 express the same lengthening rules, only using the <= operator.
R64 Pretonic Lengthening
a:ä <= ___ C'
T64 Pretonic Lengthening
a a C ' @
ä @ C ' @
---------
1: 1 2 1 1 1
2: 1 2 3 1 1
3: 1 2 1 0 1
R65 Tonic Lengthening
a:ä <= ' ___
T65 Tonic Lengthening
' a a @
' ä @ @
-------
1: 2 1 1 1
2: 2 1 0 1
In table T64 under the a:@ header, there
are transitions back to state 2 in both state 2 and state 3. This is
due to backlooping.
Rules R64 and R65, being <= rules, do not conflict, since each allows the a:ä correspondence in environments other than its own. Nevertheless, if the analyst so chooses, they can be combined into one table:
R66 Pretonic and Tonic Lengthening
a:ä <= [ ___ C'| ' ___ ]
T66 Pretonic and Tonic Lengthening
a a C ' @
ä @ C ' @
---------
1: 1 3 1 2 1
2: 1 0 1 2 1
3: 1 3 4 2 1
4: 1 3 1 0 1
R67 Nasal Assimilation
N:m <=> ___ p:
T67 Nasal Assimilation
N N p @
m @ @ @
-------
1: 3 2 1 1
2: 3 2 0 1
3. 0 0 1 0
R68 Stop Voicing
p:b <=> :m ___
T68 Stop Voicing
@ p p @
m b @ @
-------
1: 2 0 1 1
2: 1 1 0 1
These rules relate the lexical sequence Np to the surface
sequence mb. Note carefully that the symbol
p: in rule R67 is expressed as the
column header p:@ in table T67, and the
symbol :m in rule R68 is expressed as
the column header @:m in table T68. (See
section A1.7 on
overspecification in rules of this type.)
Now assume that the lexical sequence Nb is realized as the surface sequence mb (that is, both lexical Np and Nb are realized as surface mb). This shows that the N:m correspondence is found before a surface b that realizes either a lexical p or b. The distribution of the p:b correspondence is the same. Rule R67 then must be revised as follows:
R67a Nasal Assimilation
N:m <=> ___ :b
T67a Nasal Assimilation
N N @ @
m @ b @
-------
1: 3 2 1 1
2: 3 1 0 1
3. 0 0 1 0
Unfortunately, if a description containing tables T67a and T68 is given the lexical
input form aNpa, it produces not only the expected surface
form amba but also the incorrect form anpa.
The reason for this failure is similar to the problem of
overspecification discussed in section A1.7. Notice the symmetrical,
interlocking relationship between rules R67a and R68. The environment of each rule is the surface
character of the correspondence part of the other rule; that is, the
environment of rule R67a is :b, which
is the surface character of the p:b correspondence of rule
R68, and the environment of R68 is
:m, which is the surface character of the N:m
correspondence of rule R67a. This means, with
respect to the lexical form aNpa, that rule R67a does not require N to be realized as
m before a p that is realized as anything
other than b, and rule R68 does not
require p to be realized as b after an
N that is realized as anything other than m.
Thus the form aNpa can pass through the two rules
vacuously. Assuming that the analyst is correct in positing surface
environments for these two rules, the only way to fix the problem is to
prohibit the sequence N:n p:p. This can be done either by
adding the rule N:n /<= ___ p, or by incorporating this
prohibition into one of the existing tables. For example, we can revise
table T67a as follows:
T67b Nasal Assimilation
N N @ p @
m @ b p @
---------
1: 3 2 1 1 1
2: 3 1 0 0 1
3. 0 0 1 0 0
By including the column header p:p (or perhaps
@:p) in table T67b, we can recognize
N:@ p:p and force failure. Now the lexical form
aNpa will match only the surface form amba.
(Alternatively, table T68 could be revised to include
the column header N:n and fail when the sequence N:n
p:@ is recognized.)
R69 Intervocalic Voicing
p:b => V ___ V
R70 Voicing after nasal
p:b => m ___
Since the rule operator => means that the correspondence can occur
only in the specified environment, rules R69 and R70 contradict each other. The simplest resolution of
the conflict is to combine the two rules into one rule with a
disjunctive environment:
R71 Voicing
p:b => [ V ___ V | m ___ ]
The state table for rule R71 looks like this:
T71 Voicing
V m p @
V m b @
-------
1: 2 4 0 1
2: 2 4 3 1
3. 2 0 0 0
4: 2 4 1 1
where states 1, 2, and 3 correspond to the V ___ V part of
rule R71 and states 1 and 4 correspond to the
m ___ part.
Now assume that rules R69 and R70 have been initially written as <=> rules:
R72 Intervocalic Voicing
p:b <=> V ___ V
R73 Voicing after nasal
p:b <=> m ___
Their state tables look like this:
T72 Intervocalic Voicing
V p p @
V b @ @
-------
1: 2 0 1 1
2: 2 4 3 1
3: 0 0 1 1
4. 2 0 0 0
T73 Voicing after nasal
m p p @
m b @ @
-------
1: 2 0 1 1
2: 2 1 0 1
A description containing tables T72 and T73 will not work, because the => sides of the rules
conflict, just like rules R69 and R70. There are two ways to resolve the conflict between
rules R72 and R73. First, the rules
can be separated into their <= parts and => parts, and the =>
parts combined as above:
R74 Intervocalic Voicing
p:b <= V ___ V
R75 Voicing after nasal
p:b <= m ___
R76 Voicing
p:b => [ V ___ V | m ___ ]
State tables are easily written for rules R74 and R75 (not included here), and table T71
encodes rule R76 (same as rule R71).
The second way to resolve the conflict between rules R72 and R73 is to modify the environment of each table to allow the environment of the other. Tables T72 and T73 are revised as T72a and T73a.
T72a Intervocalic Voicing
V p p m @
V b @ m @
---------
1: 2 0 1 5 1
2: 2 4 3 5 1
3: 0 0 1 5 1
4. 2 0 0 0 0
5: 2 1 1 5 1
T73a Voicing after nasal
m p p V @
m b @ V @
---------
1: 2 0 1 3 1
2: 2 1 0 3 1
3: 2 1 1 3 1
Table T72a contains the column header
m:m from table T73, and table T73a contains the column header V:V from
table T72. This enables the sequence m:m
p:b to pass vacuously through table T72a and
the sequence V:V p:b V:V to pass vacuously through table
T73a.
It should also be noted that tables T72a and T73a can be combined into a single table that expresses the disjunctive rule p:b <=> [ V ___ V | m ___ ]. This can be done by dispensing with table T73a and placing a zero in the cell at the intersection of row 5 and the p:@ column of table T72a. However, when dealing with very complex rules with perhaps more than one conflict, it may be clearer to keep the rules separate as shown above.
The second type of rule conflict is the <= (or realization) conflict. It arises when two conditions are met: (1) the correspondence parts of two <= rules have the same lexical character but different surface realizations of it, and (2) the environment of one rule is subsumed by the environment of the other rule. For example, to account for the following correspondences, we posit rules R7 and r78 (where Z stands for a voiced alveopalatal grooved fricative):
LR: asa isi
SR: aza iZi
R77 Intervocalic Voicing
s:z <= V ___ V
R78 Palatalization
s:Z <= i ___ i
These rules meet both conditions of a <= conflict. First, the lexical
characters of their correspondence parts are the same (namely
s), while the surface characters are different
(z and Z). Second, because
i is a member of the subset V, the
environment of rule R77 subsumes the environment of
rule R78; that is, i ___ i is a specific
instance of the more general environment V ___ V. The state
tables for rules R77 and R78 are as
follows:
T77 Intervocalic Voicing
V s s @
V z @ @
-------
1: 2 1 1 1
2: 2 1 3 1
3: 0 1 1 1
T78 Palatalization
i s s @
i Z @ @
-------
1: 2 1 1 1
2: 2 1 3 1
3: 0 1 1 1
Given the lexical input form asa, only rule R77 will apply and return the correct surface form
aza. Given the lexical form isi, we want rule
R78 to apply and produce the surface form
iZi, but in fact the rules fail to return any
result. This is because rule R77 disallows
s:Z between vowels (including i's),
while rule R78 disallows s:z between
i's. Also, the rules cannot produce the surface form
izi, because this contradicts rule R78,
which states that s must be realized as
Z.
In generative phonology this type of conflict is resolved by ordering the specific rule before the general rule, in this case Palatalization before Voicing. Rule ordering is of course not available in the two-level model. To resolve a <= conflict in a two-level description, the general rule must be altered to allow (but not require) the correspondence of the specific rule to occur in its environment. Table T77 must therefore be revised as T77a.
T77a Intervocalic Voicing
V s s s @
V z @ Z @
---------
1: 2 1 1 1 1
2: 1 1 3 1 1
3: 0 1 1 1 1
In table T77 the column header s:@ stands
for the set of correspondences s:s and
s:Z, but in table T77a the
inclusion of the header s:Z restricts the meaning
of s:@ to only s:s. Thus the occurrence of
s:Z is not restricted by table T77a. Now s will be realized as
Z in the environment i ___ i because
table T77a allows it and table T78
requires it.
First, as the term optional suggests, a => rule is used in cases where two surface characters are truly in free variation, regardless of morphological or lexical context. For example, in many dialects of American English t is in free variation with an alveolar flap D when it occurs after a vowel and before an unstressed vowel; for example, the word writer can be pronounced either [r'aytêr] or [r' ayDêr]. This is expressed by a => rule such as rule R79 (where the absence of the stress symbol (') indicates no stress). Such rules of free variation are typically low-level phonetic rules.
R79 Flapping
t:D => V ___ V
Second, a => rule may be used in cases where a correspondence is
restricted to certain lexical items or classes of lexical items (for
instance, nouns or verbs), or to certain morphological contexts (for
instance, nominative case). For example, English needs a rule for the
f:v correspondence in pairs of words such as
wife and wives, leaf and
leaves. But this rule is restricted to a very small and
arbitrary number of lexical items (it does not apply to
fife, reef, and so on). The simplest solution
is to write the f:v rule as a => rule and let it
overgenerate and overrecognize. That is, it will generate and recognize
nonwords such as wifes (the plural of wife)
and fives (the plural of fife). For purposes
of testing a two-level description, the files of test data should
contain only well-formed words.
In generative phonology the solution to this problem is to mark the lexical entries of the words wife, leaf, and so on for a "positive rule exception," which says that only words so marked can undergo the f:v rule. The lexical component of PC-KIMMO does not allow lexical entries to be so marked for lexical features. However, the same effect can be produced by introducing a special character (often called a diacritic) in the lexical forms of exceptional words. This character serves as the "trigger" for certain rules to apply. Thus wife and leaf could be given the lexical forms wayf* and liyf* while fife and reef would have the lexical forms fayf and riyf. The f:v rule would then be written like this (where +z stands for the plural morpheme):
R80 f:v <=> ___ *:0 +:0 zWhile this solution works, it has the undesirable effect of positing lexical representations that contain nonphonological elements. Many linguists would reject such representations on theoretical grounds. (A similar solution is to posit lexical forms such as wayF and liyF and a rule for F:v. The same linguistic objections apply.)
Third, a => rule is used to "clean up" <= rules. This is a nonobvious but very important use of => rules. For example, assume that a two-level description contains two obligatory rules for lengthening, namely rules R64 and R65 in section A1.6 for pretonic and tonic lengthening. While these rules may express intuitively that lengthening applies obligatorily in the specified environments, running PC-KIMMO with just these two rules will result in overgeneration. Because <= rules do not restrict the occurrence of the correspondence in other environments, rules R64 and R65 will produce forms with the a:ä correspondence in environments where they do not occur. For example, given the lexical input labad'ar, rules R64 and R65 will return both labäd'är (correct) and läbäd'är (incorrect). To prevent this type of overgeneration, <= rules must be accompanied by analogous => rules. Thus when rule R63 is added to the description containing rules R64 and R65, only correct surface forms will be generated.
As a practical procedure in developing a two-level description, the user will typically write all the obligatory <= rules for a given correspondence first. Then to correct the resulting overgeneration, the user must write a single => rule for the correspondence; it must contain as a multiple environment (to avoid => conflicts) all the contexts of the <= rules for the correspondence.
As another example of the use of => rules as "clean-up" rules, consider again an example used in section A1.6 where the vowel of the ultimate syllable of a word is lengthened unless it is schwa, in which case the vowel of the penultimate syllable is lengthened (for example, mamän and mamänê). Assume these subsets:
SUBSET V i a u ê SUBSET Vlng ï ä üand these special correspondences:
Lengthening correspondences
i a u @
ï ä ü @
-------
1: 1 1 1 1
Following the procedure described above, assume that this is an
obligatory process. Here is the <= rule and its state table:
R81 Lengthening
V:Vlng <= ___ C(ê)#
T81 Lengthening
V V C ê # @
Vlng @ C ê # @
--------------
1: 1 2 1 1 1 1
2: 1 2 3 1 1 1
3: 1 2 1 4 0 1
4: 1 2 1 1 0 1
Now to prevent the overgeneration of ill-formed surface forms such as
mämän and mämänê,
this "clean-up" => rule must be included:
R82 Lengthening
V:Vlng => ___ C(ê)#
T82 Lengthening
V C ê # @
Vlng C ê #&@
------------
1: 2 1 1 1 1
2. 0 3 0 0 0
3. 0 0 4 1 0
4. 0 0 0 1 0
R83 Intervocalic voicing
s:z lt;=gt; V ___ V
T83 Intervocalic voicing
V s s + @
V z @ 0 @
-------------
1: 2 0 1 1 1
2: 2 4 3 2 1
3: 0 0 1 3 1
4. 2 0 0 4 0
(Notice that rows 1--3 encode the <= part of the rule and rows 1--2
and 4 encode the => part.) This table will allow a morpheme boundary
at any point in the lexical form, for instance sa+za and
saz+a.
It should be noted that generative descriptions do use explicit morpheme boundaries in rules; in such cases the rule only applies in the presence of the boundary. Often this is done to limit the rule's application to a specific morpheme by actually "spelling out" the morpheme in the rule's environment. This trick is necessary also in PC-KIMMO, since PC-KIMMO does not allow the application of rules to be limited to certain lexical items by means of lexical features. For example, the English prefix in+ has the allomorphs il+ and ir+ in words such as illegal and irregular (compare intolerable). But we do not want to write a rule that changes n to l or r everywhere (compare unlawful, inlet, enlarge, unreal). Therefore we write the => rule and table for n:l to limit the application of the rule to the lexical form in+. (The rule could be made even more specific by requiring the prefix to be word-initial.)
R84 n:l => i ___ +l
T84 i n + l @
i l 0 l @
-------------
1: 2 1 1 1 1
2: 2 3 1 1 1
3. 0 0 4 0 0
5. 0 0 0 1 0
As an example of how to encode phonotactic constraints as state tables, consider a language that allows words of the phonological shape CV(C)CV(C). That is, a word minimally consists of two open (CV) syllables, each of which can optionally be closed by a consonant. Possible words are baba, bamba, bambam, and so on. The following state table restricts all words to this pattern:
T85 CV(C)CV(C) pattern
# C V @
# @ @ @
-------
1: 2 1 1 1
2. 0 3 0 2
3. 0 0 4 3
4. 0 5 0 4
5. 0 6 7 5
6. 0 0 7 6
7. 1 8 0 7
8. 1 0 0 8
By using the column headers C:@ and V:@ rather
than C:C and V:V, table T85 is a statement of phonotactic constraints on
lexical forms, not surface forms. Phonological rules such as deletions
could result in surface forms that do not conform to the lexical-level
phonotactic pattern. To allow for diacritics such as stress ('), the
@:@ column in table T85 ignores all
symbols that are not either consonants or vowels. Thus a word such as
bab'a is allowed by the table.
As another example, we will attempt to describe the constraints on initial consonant clusters in English. First we will define the following subsets for voiceless stops (P), liquids (L), and nasals (N):
SUBSET P p t k c SUBSET L l r SUBSET N m nWe want to allow word-initial clusters of the following types: sP, sL, sN, sPL, and PL. These constraints on clusters at the lexical level are encoded in table T86.
T86 Word-initial consonant cluster constraints
# s P L N V C @
# @ @ @ @ @ @ @
---------------
1: 2 1 1 1 1 1 1 1
2: 1 3 4 5 5 1 5 2
3. 0 0 4 5 5 1 0 3
4. 0 0 0 5 0 1 0 4
5. 0 0 0 0 0 1 0 5
Table T86 will allow the lexical forms of words such
as spit, slit, snip,
prick, click, split,
string, and so on, but disallow sbit,
slpit, spmit, mlik, and so on.
Unfortunately, it will also allow nonoccurring words such as
srit, tlick, and sklit (though
scl does occur in words of Greek origin, for instance
sclera). To disallow these, another table can encode
refinements to the above table:
T87 More initial consonant cluster constraints
# s t k l r N V C @
# @ @ @ @ @ @ @ @ @
-------------------
1: 2 1 1 1 1 1 1 1 1 1
2: 1 3 4 1 1 1 1 1 1 2
3. 0 0 4 4 1 0 1 1 1 3
4. 0 0 0 0 0 1 0 1 0 4
(Note that tables T86 and T87
disallow the clusters sph and sv, which occur
in words of foreign origin such as sphere and
svelte.)