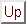
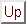


Section A2 explains how two-level rules operate, how they can be implemented as finite state machines, and how the four types of two-level rules can be translated into finite state tables.
R29 t:c => ___ iThe operator => in this rule means that lexical t is realized as surface c only (but not always) in the environment preceding i:i.
The correspondence t:c declared in rule R29 is a special correspondence. A two-level description containing rule R29 must also contain a set of default correspondences, such as t:t, i:i, and so on. The sum of the special and default correspondences are the total set of valid correspondences or feasible pairs that can be used in the description.
If a two-level description containing rule R29 (and all the default correspondences also) is applied to the lexical form tati, the PC-KIMMO generator would proceed as follows to produce the corresponding surface form.
Beginning with the first character of the input form, it looks to see if there is a correspondence declared for it. Due to rule R29 it will find that lexical t can correspond to surface c, so it will begin by positing that correspondence.
LR: t a t i
|
Rule: 29
|
SR: c
At this point the generator has entered rule R29. For
the t:c correspondence to succeed, the generator must find
an i:i correspondence next. When the generator moves on to
the second character of the input word, it finds that it is a lexical
a; thus rule R29 fails, and the
generator must back up, undo what it has done so far, and try to find a
different path to success. Backing up to the first character, lexical
t, it tries the default correspondence t:t.
LR: t a t i
|
Rule: |
|
SR: t
The generator now moves on to the second character. No correspondence
for lexical a has been declared other than the default, so
the generator posits a surface a.
LR: t a t i
| |
Rule: | |
| |
SR: t a
Moving on to the third character, the generator again finds a lexical
t, so it enters rule R29 and posits a
surface c.
LR: t a t i
| | |
Rule: | | 29
| | |
SR: t a c
Now the generator looks at the fourth character, a lexical
i. This satisfies the environment of rule R29, so it posits a surface i, and exits
rule R29.
LR: t a t i
| | | |
Rule: | | 29 |
| | | |
SR: t a c i
Since there are no more characters in the lexical form, the generator
outputs the surface form taci. However, the generator is
not done yet. It will continue backtracking, trying to find alternative
realizations of the lexical form. First it will undo the
i:i correspondence of the last character of the input
word, then it will reconsider the third character, lexical
t. Having already tried the correspondence
t:c, it will try the default correspondence
t:t.
LR: t a t i
| | |
Rule: | | |
| | |
SR: t a t
Now the generator will try the final correspondence i:i and
succeed, since rule R29 does not prohibit
t:t before i (rather it prohibits
t:c in any environment except before i).
LR: t a t i
| | | |
Rule: | | | |
| | | |
SR: t a t i
All other backtracking paths having failed, the generator quits and
outputs the second surface form tati.
The procedure is essentially the same when two-level rules are used in recognition mode (where a surface form is input and the corresponding lexical forms are output).
An FSA is composed of states and directed transition arcs. There must minimally be an initial state, a final state, and an arc between them. A successful transition from one state to the next is possible when the next symbol of the input string matches the symbol on the arc connecting the states. For example, consider the regular language L1 consisting of the symbols a and b and the "grammar" abNa where N >= 0. Well-formed strings or "sentences" in this language include aa, aba, abba, abbba, and so on. The language L1 is defined by the FSA in figure A2.
State 1 is the initial state and state 3 is the final state (signified by the double circle). States 1 and 2 are both nonfinal states (signified by the single circle). To recognize the string abba, proceed as follows:
An FSA can also be represented as a state transition table. The FSA above is represented as this state table:
a b
----
1. 2 0
2. 3 2
3: 0 0
The rows of the table represent the three states of the FSA diagram,
with the number of the final state marked with a colon and the numbers
of the nonfinal states marked with periods. The columns represent the
arcs from one state to another; the symbol labeling each arc in the FSA
diagram is placed as a header to the column. The order of the columns
in the table has no effect on the operation of the table, but is
written to reflect the order of the FSA. Notice that the two
a arcs in the FSA diagram are represented as a single
column labeled a. The cells at the intersection of a row
and a column indicate which state to make a transition to if the input
symbol matches the column header. Zero in a cell indicates that there
is no valid transition from that state for that input symbol; in the
FSA diagram this is equivalent to having no arc labeled with that input
symbol. The machine is said to fail when this happens, thus rejecting
the input form. Note that the colon marks state 3 as the only final
state. This means that if the machine is in any state but 3 when the
input string is exhausted, the string is not accepted. The 0
transitions in state 3 say that once the machine gets to that state,
the string is not accepted if there are remaining input symbols.
An FSA operates only on a single input string. A finite state transducer (FST) is like an FSA except that it simultaneously operates on two input strings. It recognizes whether the two strings are valid correspondences (or translations) of each other. For example, assume the first input string to an FST is from language L1 above, and the second input string is from language L2, which corresponds to L1 except that every second b is c. Here is an example correspondence of two strings:
L1: abbbba L2: abcbcaFigure A3 shows the FST in diagram form. Note that the only difference from an FSA is that the arcs are labeled with a correspondence pair consisting of a symbol from each of the input languages.
Figure A3 FST diagram for the
correspondence between languages L1 and L2
FSTs can also be represented as tables, the only difference being that the column headers are pairs of symbols, such as a:a and b:c. For example, the following table is equivalent to the FST diagram in figure A3.
a b b
a b c
-----
1. 2 0 0
2. 4 3 0
3. 4 0 2
4: 0 0 0
Consider rule R30.
R30 t:c => ___ iIn terms of FSTs, this rule defines two "languages" that are translations of each other. The "upper" or lexical language specifies the string ti; the "lower" or surface language says that ci may correspond to it. Note, however, that a two-level rule does not specify the grammar of a full language. Rather it deals with allowed substrings. A possible paraphrase of rule R30 is, "If ever the correspondence t:c occurs, it must be followed by i:i." In other words, if anything other than t:c occurs, this rule ignores it. This fact must be incorporated into our translation of a two-level rule into a transition diagram, shown in figure A4. In this FST, state 1 is both the initial and only final state. The @:@ arc (where @ is the ANY symbol, see section A1.3) allows any pairs to pass successfully through the FST except t:c and i:i.
Figure A4 FST diagram of a => rule
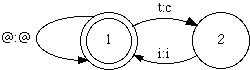
Rule R30, represented as the FST in figure A4, translates into the following state table, labeled T30. (In the remainder of this chapter, each rule and its corresponding state table have the same label number, for instance R30 and T30.) Notice that state 1, the initial state, is a kind of "default" state that ignores everything except the substring crucial to the rule.
T30 Example of a => table
t i @
c i @
-----
1: 2 1 1
2. 0 1 0
A set of two-level rules is implemented as a system of parallel FSTs
that specify all the feasible pairs and where they can occur. A state
table is constructed such that the entire set of feasible pairs in the
description is partitioned among the column headers with no overlap.
That is, each and every feasible pair of the description must belong to
one and only one column header. Table T30 specifies
the special correspondence t:c and the environment in
which it is allowed. The @:@ column header in table T30 matches all the feasible pairs that are defined by
all other FSTs of the system. Thus, with respect to table T30, @:@ does not stand for all feasible
pairs; rather it stands for all feasible pairs except t:c
and i:i.
The default correspondences of the system must be declared in a trivial FST like table T31 (see section A3.2 (step 2) and section A4.4):
T31 Table of default correspondences}
p t k a i u @
p t k a i u @
-------------
1: 1 1 1 1 1 1 1
Even this table of default correspondences must include @:@
as a column header. Otherwise it would fail when it encountered a
special correspondence such as t:c. This is due to the
fact that all the rules in a two-level description apply in parallel,
and for each character in an input string all the rules must succeed,
even if vacuously. Now given the lexical form tatik,
tables T30 and T31 will work
together to generate the surface forms tatik and
tacik.
To understand how to represent two-level rules as state tables, we must understand what the two-level rules really mean. (See section A1.5 above.) We tend to think of two-level rules positively, that is, as statements of where the correspondence succeeds. In fact, state tables are failure-driven; they specify where correspondences must fail. It is natural to think of rule R30 as saying that the correspondence t:c succeeds when it occurs preceding i:i. But state table T30 actually works because it fails when anything but i:i follows t:c (the zeros in state 2 indicate that the input has failed). This reorientation to thinking of phonological rules as failure-driven is one of the most difficult barriers to overcome in learning to write two-level rules and state tables, but it is the primary key to success with PC-KIMMO.
In summary, the rule type L:S => E (where L:S is a lexical:surface correspondence and E is an environment) positively says that L is realized as S only in E. Negatively it says that L realized as S is not allowed in an environment other than E. The state table for a => rule must be written so that it forces L:S to fail in any environment except E. In logical terms, the => operator indicates conditionality, such that, if L:S exists, then it must be in E.
R32 t:c <= ___ iThis rule says that lexical t is always realized as surface c when it occurs before i:i, but not only before i:i. Thus the lexical form tati will successfully match the surface form taci but not tati. Note, however, that it would also match caci since it does not disallow t:c in any environment. Rather, its function is to disallow t:t in the environment of a following i:i. Remembering that state tables are failure-driven, the strategy of writing the state table for rule R32 is to force it to fail if it recognizes the sequence t:t i:i. This allows the correspondence t:c to succeed elsewhere. The state table for rule R32 looks like this:
T32 Example of a <= table
t t i @
c t i @
-------
1: 1 2 1 1
2: 1 2 0 1
In state 1 any occurrences of the pairs t:c,
i:i, or any other feasible pairs are allowed without
moving from state 1. It is only the correspondence t:t
that forces a transition to state 2, where all feasible pairs succeed
except i:i (the zero in the i:i column
indicates that the input has failed). Notice that state 2 must be a
final state; this allows all the correspondences except
i:i to succeed and return to state 1. Also notice that in
state 2 the cell under the t:t column contains a two. This
is necessary to allow for the possibility of a tt sequence
in the input form; for instance, table T32 will
apply to the lexical form tatti to produce the surface
form tatci. This phenomenon is called backlooping and is
treated in detail in section T32 is potentially overspecified. It
is not really the pair t:t that is disallowed before
i, but rather the pair t:¬c; that is,
lexical t and surface not-c (anything but
c). Suppose our two-level description also contained a
rule that defined a t:n correspondence. Like
t:t, t:n should fail before i:i.
Rather than add another column for t:n to table T32, we can replace the column header t:t
with t:@. Given that the more specific correspondence
t:c is also declared in the table, t:@ will
match all other valid surface correspondences to lexical
t, such as t:t, t:n, and so on.
Here is table T32 revised to use a t:@
column header.
T32a A <= table
t t i @
c @ i @
-------
1: 1 2 1 1
2: 1 2 0 1
In summary, the rule type L:S <= E positively says that
L is always realized as S in E.
Negatively it says that L realized as any character but
S is not allowed in E. The state table for a
<= rule must be written so that it forces all correspondences of
L with anything but S to fail in
E. Logically, the <= operator indicates that if
L is in E, then it must correspond to
S.
R33 t:c <=> ___ iThe state table for a <=> rule is simply the combination of the <= and the => tables. The state table for rule R33 is built by combining tables T32a and T30 to produce table T33 below. The column headers of table T33 are the same as table T32a. States 1 and 2 represent the <= part of the table (corresponding to table T32a) while states 1 and 3 represent the => part (corresponding to table R30).
T33 Example of a <=> table
t t i @
c @ i @
-------
1: 3 2 1 1
2: 3 2 0 1
3. 0 0 1 0
In summary, the rule type L:S <=> E says that
L is always and only realized as S in
E. It implies that L:S is obligatory in
E and occurs nowhere else. The state table for a <=>
rule must be written so that it forces all correspondences of
L with anything but S to fail in
E, and forces L:S to fail in any environment
except E.
R34 t:c /<= ___ i:êThis rule states that the correspondence t:c is disallowed when it precedes a lexical i that is realized as a surface ê. As the /<= operator suggests, this rule type shares properties of the <= type rule. It states that the correspondence always fails in the specified environment, but allows it (does not prohibit it) in any other environment. The strategy for building a state table for the /<= rule is to recognize the correspondence in the specified environment and then fail. In table R34 the correspondence t:c forces a transition to state 2 where the table fails if it encounters the environment i:ê, but succeeds otherwise. Notice that like table T32 above for a <= rule, state 2 is final.
T34 Example of a /<= table
t i @
c ê @
-----
1: 2 1 1
2: 2 0 1
In summary, the rule type L:S /<= E positively says that
L is never realized as S in E.
Negatively it says that L realized as S is
not allowed in E. Logically, the /<= operator indicates
that if L is in E, then it must correspond to
¬S.