Going Further 16.3: Why the Flatness Problem is a Problem

The coincidence of a flat Universe, or in other words, one with a density equal to the critical density, is quite special. Since there is no particular reason that the Universe should be close to the critical density, it is strange that it does lie so close.

If the density of the Universe is equal to the critical density, the expansion rate exactly equals the rate needed to make the Universe flat, so the Universe would expand forever but at a velocity always slowing towards zero. Understanding why this is the case is difficult without mathematics, so let’s try a simplified illustration.

This is analogous to the Newtonian notion of the escape speed from a planet. For illustrative purposes we can replace our expanding Universe with a single object leaving a planet at escape velocity, depicted in Figure B.16.3. The physics will be qualitatively the same, but the mathematical treatment is much simpler. If we reduced that object’s velocity by 1% it would no longer escape but would turn around and fall back. For example, if we launch a rock off of Earth’s surface at 99% of the escape speed, the rock would get almost all the way to the Moon before it stopped and fell back to Earth.

If we fancifully imagine that the planet at earlier times was compressed to smaller radii (the way the size of the Universe is smaller at earlier times), then we will find a striking effect. Launching our rock with the same 99% of the escape velocity for a compressed planet will hardly raise it off the surface at all before it falls back. For example, to get to the Moon’s orbit with a compressed Earth, we would have to launch our projectile object with a higher velocity, greater than 99% though still slightly less than the escape velocity. The following activities show why this is the case.

In this Newtonian example, the velocity of the object gets closer and closer to the escape speed as a planet gets smaller. This is analogous to the density of the Universe getting closer and closer to the critical density as the size of the Universe shrinks at earlier times.

Figure B.16.3: Object Launched from a Planet Surface

If an object with mass m is launched at some velocity v from the surface of a planet with mass M, how far up does it go before it stops and falls back down? Credit: NASA/SSU/Aurore Simonnet

If an object of mass m is thrown upward with speed v from the surface of a planet it will have a total energy (Etot), which is a combination of kinetic and potential energy, given by:

\begin{equation} E_{tot}=\frac{1}{2}mv^2 - \frac{GMm}{R} \end{equation}

Here M is the mass of the planet and R is its radius. If we assume that the velocity is less than the escape velocity and the projectile eventually rises to the point r, then the total energy can also be written as:

\begin{equation} E_{tot}= - \frac{GMm}{r} \end{equation}

Setting these two expressions equal to each other we get

\begin{equation} \frac{GMm}{r}= \frac{1}{2} mv^2- \frac{GMm}{R} \end{equation}

The escape velocity is found by setting the total energy to zero. (In that case the object will eventually have no kinetic energy, and its potential energy will be zero since r will become infinite.) But we are not looking for the escape speed here, we wish to know how high the object travels before it stops and falls back.

We can cancel the common factor of m from each term, and then solve for r:

\begin{equation} \frac{GM}{r}= \frac{1}{2} v^2- \frac{GM}{R} \end{equation}

and rearranging:

\begin{equation} r= \frac{-GM}{\frac{1}{2}v^2-\frac{GM}{R}} \end{equation}

This expression can be greatly simplified by factoring out the GM / R from the denominator:

\begin{equation} r= \frac{-GM}{\frac{GM}{R} \left(\frac{Rv^2}{2GM} - 1\right)} \end{equation}

Now we can cancel the common term of GM from the numerator and denominator and raise the factor of 1 / R from the denominator into the numerator. In addition, we see that there is a factor of the escape velocity in the denominator: v2esc = 2GM / R. Thus we can simplify as follows:

\begin{equation} r= \frac{-R}{\left (\frac{v}{v_{esc}}\right )^2-1} \end{equation}

Now we can tidy up a bit by canceling a factor of -1 from the numerator and denominator of the fight-hand side, and dividing through by R to get a final expression for how high an object rises given a planet’s size and the object’s velocity:

\begin{equation} \frac{r}{R}= \frac{1}{1- \left (\frac{v}{v_{esc}}\right )^2} \end{equation}

We can use this expression to determine how high an object will rise if launched from Earth, as in the following worked examples.

 

1. How far will an object rise off the surface of a planet (relative to the planet’s radius) if it’s launched at 90% of the escape velocity?

This means it will rise to 5.26 times the planet’s radius.

 

2. How far will an object rise off the surface of a planet (relative to the planet’s radius) if it’s launched at 99% of the escape velocity?

This means it will rise to 50 times planet’s radius.

 

So the object will rise to about fifty times the radius of the object from which it is launched.

 

3. How far is this for Earth, which has a radius of 6400 km?

This is nearly the distance to the moon.

 

We can also plot the distance reached (r/R) versus launch velocity (v/vesc). To create the graph, we can calculate r/R for several values of v/vesc, as in Table B.16.1.

 

Table B.16.1. Velocity and peak height of an object launched from a planet.

v/vesc

r/R

0.0

1.0

0.2

1.04            

0.4

1.19

0.6

1.56

0.8

2.78

0.9

5.26

0.95

10.26

 

 

From this table, we use the Graphing Tool to graph r/R vs. v/vesc in Figure B.16.4.

 

Figure B.16.4 height and escape speed

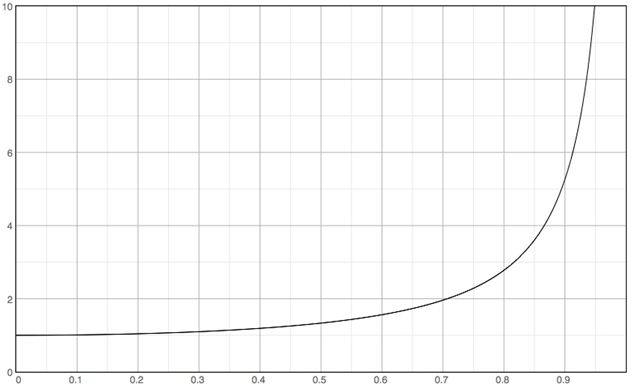
The ratio of the height attained to the radius of the planet as a function of velocity in terms of escape speed. Credit: NASA/SSU

 

From this graph, we can answer the several questions. You will see that the ratio of launch velocity to escape velocity becomes much more sensitive to deviations from 1.0 as an object shrinks. This is analogous to the expansion of the Universe; the Universe must be very exquisitely balanced near its critical density in order for it to be so close to that density today.

 

  1. Why is the height attained equal to 1 when the launch velocity is zero?

 

Since the projectile begins at r = R, if it has zero initial velocity it never leaves the surface, so r/R = 1 at its highest point.

 

  1. Explain why the height seems to rise without bound as the launch velocity (in terms of escape velocity) approaches 1.

 

When v = vesc the projectile is able to escape to infinity, thus as the launch speed approaches that value the height attained approaches infinity.

 

  1. How does the height reached by a projectile depend on the speed at which it is launched? 

 

As the speed becomes a larger fraction of escape speed the height attained increases, regardless of the size of the planet. The answer does not depend on the size of the planet because both axes on the graph are in terms of the planet’s size. The escape speed includes all of the relevant information on the planet’s mass and radius, and the height attained is in terms of the planet radius, so any dependence on planetary parameters are hidden by this method of plotting.

 

  1. As the planet gets smaller, what must happen to the launch velocity in order to cause the physical height reached by the projectile to remain constant?

 

If the projectile is to reach a constant value of r as the size of the planet (R) decreases, then its velocity as a fraction of escape speed must increase. Thus the absolute launch speed must also increase.

 

  1. In this exercise, escape velocity is analogous to the critical density of the Universe. How does this exercise demonstrate that, if the density of the Universe today is close to the critical density, it must have been even closer to critical density in the past?

 

The escape speed of a planet of given mass will increase as the planet is made smaller. That means that if an object is near escape speed on a large planet, it must be even nearer escape speed on a smaller planet of the same mass in order to reach a similar height. The ratio v/vesc must approach 1 as the planet gets smaller in a way similar to the way that ρ/ρcrit must approach 1 as we look further into the past when the scale factor of the Universe was smaller than it is today.