4.9 Algorithms

4.9.1 The Generator

4.9.2 The Recognizer

Figure 4.22 A lexical letter tree

The algorithms used by PC-KIMMO to generate and recognize are based on descriptions in Karttunen 1983. These algorithms pertain only to the rules and lexical components, not the word grammar component.

4.9.1 The Generator

Lexical form:

Initially the input form, this string contains whatever is left to process. As the function is recursively called, this string gets shorter as the result string gets longer.

Result:

Initially empty, this string contains the results of the generator up to the point of the current function call.

Rules:

This is the set of active finite state automata defined for this language.

Configuration:

This is an array representing the current state of all rules (automata). Initially, all states are set to 1.

The generator function also uses a list of feasible pairs sanctioned by the set of rules; these are all the lexical:surface pairs of alphabetic characters that appear as column headers in the state tables. The input pair is a feasible pair selected by the generator as a possible next lexical:surface pair in the process of computing a surface form that corresponds to the given lexical form. Each time the generator is called it iteratively goes through the list of feasible pairs, selecting one as the input pair.

The generator algorithm works as follows:

1. If the lexical form is empty (that is, there are no more characters in it to process), do the following steps:
   1. If any of the state tables contains a word boundary column header, step the automata using an input pair consisting of the BOUNDARY symbol as both the lexical and surface character. If this fails, then the result is rejected and the function returns to the previous level.

   2. Check that the configuration array contains a valid final state for each of the rules. If so, then the result is accepted and added to the output list. Otherwise, it is rejected. In either case, the function returns to the previous level.

   Otherwise, if the lexical form is not empty (that is, it contains more characters to process), do steps 2 and 3.

2. For each input pair containing the first character in the lexical form as the lexical character, do the following steps:
   1. Step the automata using the input pair and the input configuration array, producing a new configuration.

   2. If this succeeds, recursively call the generator function with these inputs:

   Lexical form:

   This is the input lexical form with the first character removed.

   Result:

   This is the input result string with the surface character from the current input pair appended.

   Configuration:

   This is the state array produced by stepping the automata.

   1. If this fails, choose another input pair from the list of feasible pairs and do either step 2 or step 3.

   For each input pair containing the NULL symbol as the lexical character, do the following steps:

   1. Step the automata using the input pair and the input configuration array to produce a new configuration.

   2. If this succeeds, recursively call the generator function with these inputs:

   Lexical form:

   This is the input lexical form with no character removed (since the lexical character posited was NULL).

   Result:

   This is the input result string with the surface character from the current input pair appended.

   Configuration:

   This is the state array produced by stepping the automata.

   1. If this fails, choose another input pair from the list of feasible pairs and do either step 2 or step 3.

4.9.2 The Recognizer

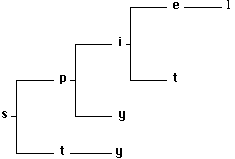
The recognizer also consults the lexicon. The lexical items recorded in the lexicon are structured as a letter tree. When the recognizer tries a lexical character, it moves down the branch of the letter tree that has that character as its head node. If there is no branch starting with that letter, the lexicon blocks further progress and forces the recognizer to backtrack and try a different lexical character. For example, Figure 4.22 is a letter tree for the lexical items spiel, spit, spy, and sty.

Figure 4.22 A lexical letter tree

Besides applying the phonological rules and identifying morphemes, the recognizer also must enforce morpheme order constraints. The PC-KIMMO lexicon is divided into classes of lexical items that behave alike with respect to order constraints. These lexical classes are called sublexicons. The entry for each lexical item specifies the name of the sublexicon that can follow it. This following sublexicon is called a continuation class. Lexical items that occur only at the end of a word have no continuation class, indicated by the BOUNDARY symbol.

The names of the sublexicons that make up the entire lexicon are used as nodes at the head of branches of the letter tree. The piece of a letter tree shown in Figure 4.22 may actually be under a branch node called Noun. When the recognizer successfully finds a lexical item in the letter tree, it looks at its specified continuation class and jumps to the branch of the lexicon it names.

It is often the case that at a given point in a word, more than one continuation is possible. Sets of alternative continuing sublexicons are called alternations. Thus the continuation class field of a lexical entry may contain the name of an alternation that specifies a list of the sublexicons that can follow it.

When the recognizer successfully recognizes a lexical item (word or morpheme), it reads its gloss from its lexical entry and appends it to the gloss string being built up for the entire word.

The recognizer function has these inputs:

Surface form:

Initially the input form, this string contains whatever is left to process. As the function is recursively called, this string gets shorter as the result string gets longer.

Result:

Initially empty, this string contains the results of the recognizer up to the point of the current function call.

Gloss:

Initially empty, this string contains glosses for the lexical items contained in the result string.

Rules:

This is the set of active finite state automata defined for this language.

Configuration:

This is an array representing the current state of all rules (automata). Initially, all states are set to 1.

Lexicon:

Initially, this is the entire lexicon defined for the language. During the process of recognition it is restricted to a branch of the lexicon.

Like the generator, the recognizer function uses a list of feasible pairs sanctioned by the set of rules; these are all the lexical:surface pairs of alphabetic characters that appear as column headers in the state tables. The input pair is a feasible pair selected by the recognizer as a possible next lexical:surface pair in the process of computing a lexical form that corresponds to the given surface form. Each time the recognizer is called it iteratively goes through the list of feasible pairs, selecting one as the input pair. When a complete lexical item has been recognized, the lexicon is at a terminal node of the letter tree. Terminal nodes have glosses and continuation classes attached to them. The recognizer algorithm is initialized as though it has successfully recognized a lexical item and the lexicon is at a terminal node pointing to a continuation class consisting of the INITIAL sublexicon. It then proceeds as follows:

1. If the input lexicon is at a terminal node, then for each sublexicon in the continuation class of that item, recursively call the recognizer function with these inputs:

   Surface form:

   This string contains whatever is left to process.

   Result:

   This string contains the results of the recognizer up to the point of the current function call.

   Gloss:

   This is the input gloss string with the gloss of the current lexical entry appended.

   Rules:

   This is the input set of rules.

   Configuration:

   This is the input configuration.

   Lexicon:

   This is the current continuation sublexicon.

   If the continuation class of the lexical entry is empty (that is, the lexical item can only be followed by word boundary) and the input surface form is empty, do the following steps:

   1. If any of the state tables contains a word boundary column header, step the automata using an input pair consisting of the BOUNDARY symbol as both the lexical and surface character. If this fails, then the result is rejected and the function returns to the previous level.

   2. Check that the configuration array contains a valid final state for each of the rules. If so, then the result is accepted, the gloss of the lexical entry is appended to the gloss, and both the result and the gloss are added to the output list. Otherwise, the result is rejected. In either case, the function returns to the previous level.

   If the continuation class of the lexical entry is empty but the surface form is not empty, the result is rejected and the function returns to the previous level.

2. For each input pair that has the head of a branch in the lexicon as the lexical character and the first character of the surface form as the surface character, do the following steps:
   1. Step the automata using the input pair and the input configuration array to produce a new configuration.

   2. If this succeeds, recursively call the recognizer function with these inputs:

   Surface form:

   This is the input surface form with the first character removed.

   Result:

   This is the input result string with the lexical character from the current input pair appended.

   Gloss:

   This is the input gloss string.

   Rules:

   This is the input set of rules.

   Configuration:

   This is the state array produced by stepping the automata.

   Lexicon:

   This is the branch of the lexicon corresponding to the lexical character from the current input pair.

   For each input pair that has the head of a branch in the lexicon as the lexical character and has the NULL symbol as the surface character, do the following steps:

   1. Step the automata using the input pair and the input configuration array to produce a new configuration.

   2. If this succeeds, recursively call the recognizer function with these inputs:

   Surface form:

   This is the input surface form.

   Result:

   This is the input result string with the lexical character from the current input pair appended.

   Gloss:

   This is the input gloss string.

   Rules:

   This is the input set of rules.

   Configuration:

   This is the state array produced by stepping the automata.

   Lexicon:

   This is the branch of the lexicon corresponding to the lexical character from the current input pair.

   If the NULL symbol is the head of a branch of the lexicon (that is, a null lexical entry), recursively call the recognizer function with these inputs:

   Surface form:

   This is the input surface form.

   Result:

   This is the input result string.

   Gloss:

   This is the input gloss string.

   Rules:

   This is the input set of rules.

   Configuration:

   This is the input state array.

   Lexicon:

   This is the branch of the lexicon which has the NULL symbol as its head.