Contents
Power Drops Within Lys
Computing MIP Levels From Specular Power/Roughness
To compute MIP level from specular power/roughness you need to have the number of MIP levels in the cube map available in your shader.
If you are developing in HLSL then you can get hold of it using GetDimensions() and if you are using GLSL then you can use textureQueryLevels().
If you are developing in a shader language where you do not have access to such built-in functions then it's suggested to pass it as a constant to your shader.
Alternatively you can compute it in shader code using the following function:
int GetNrMips(samplerCube cube_spec)
{
int top_dim = textureSize(cube_spec, 0).x;
int nMips = int(log2(float(top_dim>0 ? top_dim : 1)))+1;
return nMips;
}
Power Drops Within Lys
In the following, the power drops of Lys will be explained and we describe how to map specular power to the correct floating point MIP entry. Be sure to enable trilinear filtering when using cube maps for image based lighting to achieve continuous spec powers.
If your shader uses roughness and not specular power then you should remap using the following function:
float RoughToSPow(float fRoughness) // convert to specular power
{
return (2.0/(fRoughness*fRoughness))-2.0;
}
The Log2 Power Drop
In Lys we currently support two power drops. Default and Log2.
The goal when designing your drop curve is to get a distribution of specular power values across MIP levels that fit the needs of your application. The first thing to do is to decide at which MIP level to place the specular power of 1, which in Lys corresponds to the highest roughness.
You do this by specifying the "MIP Offset" in the specular group. This value represents an offset from the bottom 1x1 cube map MIP level.
The default value of 3 corresponds to assigning a specular power of 1 to level 8x8. To help you make the right choice you can check "Coarse Irradiance" in the 3D Preview which will then use the MIP level at your chosen offset for diffuse lighting.
Next you need to distribute the remaining specular power values. For the Log2 distribution this is done using the "User Scale".
There are two ways to observe the values you get. One is by toggling through the MIP levels in the specular group. The other is by selecting
the roughness view in the 3D Preview.
The code to convert the specular power to a MIP entry is as follows:
float GetSpecPowToMip(float fSpecPow, int nMips) // log2 distribution
{
return (nMips-1-nMipOffset) - log2(fSpecPow)*fUserScale;
}
Ultimately the goal is to pick fUserScale such that you get the distribution you need. But for numerical interpretations you could also think of
fUserScale as a change in log-base since log_a(x)=log2(x)/log2(a) which implies fUserScale is 1/log2(a)
Another convenient way of looking at it is you can assign a specific specular power N to a chosen MIP offset from the bottom mMipPivot.
To achieve this we get:
fUserScale = (mMipPivot-nMipOffset)/log2(N)
So for instance to assign a specular power of 2048 to the pivot 7 which corresponds to the MIP map resolution 128x128 we would get 4/11.
Specular Power Distrubution across Mip Map Levels
The figure shows the specular power distributions for 3 different userscales where top level is 128x128 and nMipOffset is set to 3.
Note that though MIP Level m is by convention zero at the top, the value nMipOffset (and mMipPivot) is zero at the bottom MIP level.
The Default Power Drop
The first power drop "Default" allows the user to pick a maximum specular power/roughness for the top MIP level. The curve we use for this was kindly made available to us by the Marmoset team who use it to convert from a gloss map [0;1] to a specular power inside of Marmoset Toolbag 2.
The Marmoset Toolbag 2 curve is ( -10.0 / log2( gloss*0.968 + 0.03 ) )^2 which gives a specular power range of about 4.0 to 12 Million. In the context of image based lighting this range is a bit more than we need so we adjusted the constants by making them 0.9921 and 0.00098 instead which gives us the output range of 1.0 to 999999.
Since we are going from specular power to MIP level and not the other way around we need to use the inverse function.
We also need to know the user's choice for maximum specular power fUserMaxSPow of the top MIP level.
Finally we can compute the MIP level as:
const float k0 = 0.00098, k1 = 0.9921;
// pass this as a constant for optimization
uniform float g_fMaxT = ( exp2(-10.0/sqrt( fUserMaxSPow )) - k0)/k1;
float GetSpecPowToMip(float fSpecPow, int nMips)
{
// Default curve - Inverse of TB2 curve with adjusted constants
float fSmulMaxT = ( exp2(-10.0/sqrt( fSpecPow )) - k0)/k1;
return float(nMips-1-nMipOffset)*(1.0 - clamp( fSmulMaxT/g_fMaxT, 0.0, 1.0 ));
}
Pre-convolved Cube Maps vs Path Tracers
Another detail worth noting is that pre-convolved cube maps have to be made such that the convolution process ignores the orientation of the receiving surface.
If results are compared to path tracers used for movie production quality you will find the result you get from a pre-convolved cube map, for the same specular power, is roughly 4 times more sharp.
The distinction is the path tracer will use the roughness/specular power to drive a formulation based on n_dot_h as opposed to l_dot_r where the normal is arbitrary.
For pre-convolving cube maps we are limited to l_dot_r. However, we can account for the difference in the shader by observing the relation between the solid angle of the half vector dH and the reflection vector dR which is dR = 4 * h_dot_r * dH.¹
Reflected Beam
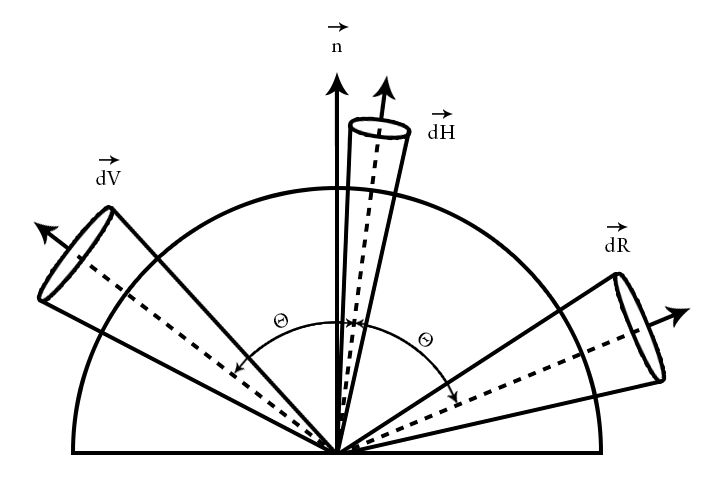
The view direction v reflected by dH will result in dR. Given the existing symmetry the central direction r of dR will result in dV when reflected by dH.
As an approximation we can correlate size of solid angle with "blur strength"and replace h_dot_r with n_dot_r. So ultimately what we do is adjust our specular power in the following way:
fSpecPow /= (4*max(dot(vN, vR), FLT_EPSILON));
This works because the specular power is roughly inversely proportional to the amount of blur.
We then use the adjusted fSpecPow to find our MIP level with GetSpecPowToMip(). This adjustment is of course just for the cube maps and should NOT be applied to the specular power used with ordinary lights since for these we simply use an n_dot_h based formulation as opposed to l_dot_r.
This approach will work with both normalized Blinn-Phong ¹ ² and GGX. In the former case use cosine weighted convolution in Lys. Though it is an approximation it gives results that are close to what the path tracer will provide for the same specular power. The approach will also harden the reflection as we approach the silhouette which is more physically correct.
Below we have set out renders ³ featuring results of Lys cube maps vs a path tracer with various specular powers/roughness. The results using Lys cube maps are set out in the top row of each image whereas the bottom row shows the results from the path tracer.
As we see using the approach described above we achieve matching results to a path tracer. The "blur strength" matches when the same specular power is used and notice how the reflection of the building on the right side hardens as we approach the silhouette of the sphere. Traditionally this requires half vector based BRDF formulations which cannot be precomputed and stored in the cube map.
Specular Powers of 32, 64, 128 & 256.

Specular Powers of 512, 1024, 2048 & 4096

Reference
[1] Morten S. Mikkelsen. Microfacet Based Bidirectional Reflectance Distribution Function.
[2] Bruce Walter, Stephen R. Marschner, Hongsong & LiKenneth E. Torrance. Microfacet Models for Refraction through Rough Surfaces.
[3] All HDRI photo based source images shown in the above were kindly provided by Marmoset.
