Lesson Three: Using Numeric Variables
There are two main types of numeric data: integers and floating-point numbers. When you assign a numeric value to a variable, the variable will automatically become an integer or floating-point data type, depending on the type of value you assign.
Integers
Integers are positive or negative whole numbers, including the number zero (0). Sometimes an integer is also called an "int" for short. There are no fractions or decimal places in an integer value. Here are some example values that can be stored as integers.
- A student’s grade level (such as 12)
- The number of brothers and sisters you have (such as 2)
- The year you were born (such as 2005)
When writing numeric values in Python code, do not use commas or other separators. A number that you might hand-write as "3,482" on paper should be typed as "3482" in your source code.
The print() function knows how to display an integer on the screen, so you could pass a hard-coded or typed-in number directly to the function. Run the example code below to see the output. Then, change the integer value to something different and try running it again.
Anywhere that you might use a hard-coded value like "45", you can also use a variable of the same type. Let's create an integer variable named myScore and assign a value to it, Then, we'll pass that integer variable into the print() function to see the results on the screen. Try it yourself!
Numeric variables must use enough computer memory to hold the integer values you assign to them. Computer memory is measured in bits (a 0 or 1 digit in the binary number system) or bytes (a collection of 8 bits). In some languages, the amount of memory assigned to a variable is fixed and cannot change. Therefore, a specific numeric variable can only hold values within a range that is defined by the amount of memory in the variable. A variable made up of a single byte, for example, could only hold the values 0 to 255 (or -128 to +127). Attempting to assign values outside the allowed range to an integer variable can result in overflow errors and other problems, which means the resulting value is not what you expect!
Fortunately, in Python, an integer variable will automatically grow to hold any size number you put inside. The size of a numeric value in Python is limited only by the amount of overall memory in your system! To test this concept, try modifying the program above to display a much larger value than 45.
The AP Computer Science Principles exam assumes that integer variables can hold values of any size, without preset limits.
Floating-Point Numbers
Floating-point values are real numbers, which are numbers that can contain an integer plus a fractional part, separated by a decimal point. Sometimes a floating-point number is also called a "float" for short. Do you see how each of the following examples should be stored in a floating-point variable?
- The math constant PI (3.14159)
- Your grade point average (3.5)
- The amount of money in your pocket ($0.75).
Floating-point values are not required to have a fractional part. The digits to the right of the decimal point may all be zero (4.00).
Just like integers, floating-point numbers should not include commas or other symbols like dollar signs. You should only use numbers and decimal points. So, the hand-written value "$1,000.50" would be written as "1000.50" in Python code.
The print() function knows how to display floating-point values, just like integers. Experiment with the following code example to see how it works.
Creating a floating-point variable and using it in place of a hard-coded value works the same way. Run the code below to create a floating-point variable named PI, store a value in it, and then print the contents of that variable to the screen.
The Python language will automatically choose the correct numeric data type based on the number that you enter in your program. Python will consider any number written without decimals as an integer (like 1000) and any number written with decimals as a floating-point (like 3.14).
Computer programs must represent floating-point numbers with bit and bytes. Some fractional values like 1/3 would be written in decimal with an infinite number of digits (0.33333...). Some finite decimal values like 0.1 are also hard to represent exactly in binary form. In both cases, Python and other languages can store a floating-point number that is very close to the original value. However, no matter how many bits you use, it will never represent the original value exactly. This means programs should understand that floating-point numbers may not be exact and can be subject to tiny round-off errors.
The type() Function
You may want to study the data type of a particular variable to see if it is an integer, floating-point or some other type. Python contains the built-in type() function that will give us this information. type() accepts a variable name between the parentheses and will return a description of the data type as a string.
In the example below, we create a floating-point variable called myValue. We then pass that variable into the type() function and store the resulting type information in another variable called myType. Finally, we print the contents of myType so we can see what information was returned. Try it yourself and see the results! Then, change the input value from 3.14 to 0 and run it again.
It is OK to pass the results from one function directly into another function. So, we could take the string results from type() and pass that directly into the print() function as shown below.
You will find that floating-point variables have a type of "<class 'float'>" and integers are described as "<class 'int'>". If you use other data types like strings, you will get similar descriptions like "<class 'str'>". We'll use the type() function in a moment to help understand the results of mathematical operations.
Math Operations
You can do basic mathematic functions like addition, subtraction, multiplication and division on your numeric variables. You can also get the remainder or modulus of a division operation. Python (and most other programming languages) uses the following special characters to perform the math operations:
| Symbol | Description | Example Statement | myResult |
|---|---|---|---|
| + | Addition | myResult = 1 + 2 | 3 |
| - | Subtraction | myResult = 5 - 3 | 2 |
| * | Multiplication | myResult = 4 * 2 | 8 |
| / | Floating-Point Division | myResult = 10 / 4 | 2.5 |
| // | Integer Division | myResult = 10 / 4 | 2 |
| % | Modulus | myResult = 10 % 3 | 1 |
A mathematical expression is formed by writing two numeric values, separated by one of the mathematical symbols +, -, *, /, //, or %. Python will perform the calculation and produce a single result value. You will most likely want to store the result in a variable, print the result to the screen, or put it to some other use.
Python will automatically examine the data types of your input values and produce a result of the correct data type. So, adding together two integers will produce an integer result, while subtracting two floating-point values will give you a floating-point result.
The examples below demonstrate using a mathematical expression directly as input to a function like print() as well as storing an expression results in a variable for future use. Try changing each math expression to experiment with all four operations (+, -, * and /). Run the code to see your results!
The forward slash (“/”) is used to divide one value with another. The left value is the dividend (the number on top that gets divided) and the right number is the divisor (number on bottom that is doing the division). Notice The results of a floating-point division operation (/) are always floating-point, even if the answer itself (like 10 / 2 = 5.0) is a whole number. If you want to produce an integer from division, dropping any fractional results, use the double slash (//) instead. Run the example below to see the difference!
Be sure that you never attempt to divide by 0, or you will receive an error when you run your program. Modify one of the expressions above to divide by 0 and look for the resulting error message.
For example, if you attempt to divide "5 / 0", you will see an error message like the one below.
Traceback (most recent call last):
File "code1.py", line 1, in <module>
print(5 / 0) # print math result directly to the screen
ZeroDivisionError: division by zero
Most Python error messages are very helpful, showing you the exact file and line number where the error happened, the statement that caused the error, and a description of the error (e.g. "division by zero"). When you see an error like this, use the information it contains to find and fix the problem in your code.
The Modulus Operator
When you perform an integer division like 7 / 3, the mathematical answer can be written as a whole number (like 2) and a remainder (like 1).
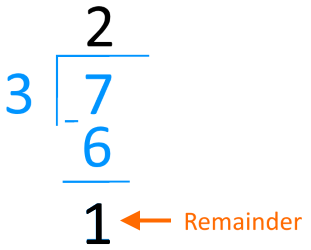
The modulus operator (%) performs an integer division of two operands and returns the remainder. The dividend comes first, followed by the percent sign % and then the divisor.
If the result of a modulus operation is 0, that means the first operator (the dividend) is evenly divisible by the second operator (the divisor) with no remainder.
Longer Expressions
You can chain together several math operations into one statement. Simply continue to add additional symbols and input values to the right of the first operation. For example, you can multiply together 4 numbers by writing the following expression.
You can even include function calls in your expressions to produce one of the terms! Remember, no matter how complex your expression is, it will only produce a single value as a result. We will discuss longer expressions in more detail in a later chapter.
Using Variables in Math Expressions
Writing hard-coded math expressions like "5 + 1" in your code is not very interesting, because the result will always be the same. Programmers will often use variables in place of one or both input values to a math expression. If you have two input values stored in variables score1 and score2, then you could write an expression to add those inputs together and store the result in a third variable.
Run the example below to see the results. Do you see how we are using variables as parts of mathematical expressions?
Operator Precedence
Consider the following statement that combines multiple math operations in the same expression.
result = 5 + 2 * 4What is the result when this statement executes? Does the program add 5 + 2 first and then multiply the result with 4 to get 28? Or does the program multiply 2 * 4 first and then add 5 to get 13?
The answers to these questions are found in the Python operator precedence rules. Operator precedence is the term that describes the order in which operators are carried out by the compiler within a single expression. The higher precedence operators are executed first within a statement, followed by the lower precedence operators.
The following table contains a list of math operators and precedence (from higher to lower) in the Python language.
| Precedence Level | Operator Name | Operator Description |
|---|---|---|
| Highest | * / % | Multiplication, Division, and Modulus |
| Lowest | + - | Addition and Subtraction |
This means in an expression like "5 + 2 * 4", the multiplication will happen first, followed by addition. So the program first calculates 2 * 4, which is equal to 8. Then the program will add 5 to 8 and assign the value 13 to the result.
If an expression has more than one operator like * and / at the same precedence level, they are executed as they appear from left to right in the expression. Let's take a look at a more complicated statement.
int x = 3 * 4 + 6 / 3 - 2;This may look difficult, but we can step through this statement one operator at a time. The highest precedence operators in this expression are the '*' and '/' operators. Since they have the same precedence the compiler will evaluate them left to right. So, our first calculation is 3 * 4, and we can substitute the answer (12) into the remaining expression.
12 + 6 / 3 - 2The division '/' operator has the highest precedence of the remaining operators, so our next calculation is 6 / 3. We can plug the answer (2) back into the expression.
12 + 2 - 2The remaining + and - operators have the same lower-level precedence, so they will be evaluated from left to right. Our next calculation is 12 + 2, which gives us:
14 - 2Finally, we can perform our last calculation, 14 - 2, which gives the final answer: x = 12.
Study the example expressions below. Try to calculate each result on your own using operator precedence rules. Then, run the code to check your answers.
Work with Me: Math Lab - Triangles
In this exercise, you are going to create numeric variables and use them in a mathematical expression to calculate the area of a triangle. The area of a triangle is equal to one half of the base multiplied by the height, or area = 0.5 * base * height.
The starting code below contains comments that ask you to write specific code on each line following the comment. Add your code in the areas shown and then click "Run Code" to verify your results.
The calculated area using a base of 10 and a height of 5.0 should be 25.0. The base variable is an integer, while the height and area variables are floating-point. Try changing the initial base and height values and confirm the new area is calculated correctly. If you need to start over, you can go back to the default code by reloading this page in your web browser.
Work with Me: Floating Point Limitations
Remember, some decimal values like 0.1 are hard for computers to store in binary form. If you try to use floating point numbers like 0.1 in a program, actual value used is very close to, but not exactly equal to 0.1. Normally, the difference is so small that you won't notice.
Study the code below. What value to you think will be printed for result1, result2, and so on?
Now, run the code and explain the behavior you are seeing.
- Why do answers for some of the results have small errors at the end?
- Why do these errors appear to be getting larger as you continue to multiply the previous result by 0.1?
- What are the consequences of using floating point values that can't be directly represented by bits? Should programs rely on getting exact results from floating-point math?