Operação de Conjuntos

Matemática

CapaUnião de ConjuntosInterseção de ConjuntosDefiniçãoReferência

MATEMÁTICA
Operação de Conjuntos

União de Conjuntos

Sejam os conjuntos A = {0,1,2,3} e B = {2,3,4,5,6}.

Podemos determinar um conjunto C formado pelos elementos que pertencem a A ou a B, ou a ambos: C = {0,1,2,3,4,5,6}. O conjunto C é chamado de união ou reunião de A e B.

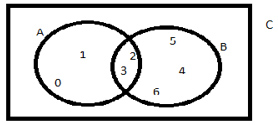
União dos conjuntos A e B em diagrama de Venn

Fonte: Elaborada pela autora

A ∪ B = {{x/ x ∈ A ou x ∈ B}

Propriedades da União e Reunião

Considerando os conjuntos A, B e C, temos as seguintes propriedades:

A ∪ A = A(idempotente)

A ∪ Ø = A (elemento neutro)

A ∪ B = B ∪ A (comutativa)

(A ∪ B) ∪ C = A ∪ (B ∪ C) (associativa)

Exemplos:

Considerando os conjuntos A, B e C, temos as seguintes propriedades:

1) {0,5} ∪ {1,2,3,4} = {0,1,2,3,4,5}

2) {1,2} ∪ {1,2,3,4} = {1,2,3,4,5}

3) {1,2,3} ∪ {3,4,5,6} = {1,2,3,4,5,6}

4) {1,2,3} ∪ ∅ = {1,2,3}

5) ∅ ∪ ∅ = ∅

Interseção de Conjuntos

Sejam os conjuntos A = {0,2,4,6} e B = {0,1,2,3,4,5}

Podemos determinar o conjunto formado pelos elementos que são comuns a A e B, ou seja, elementos que pertencem a A e que também pertencem ao conjunto B.

Assim, temos que A ∩ B = {0,2,4}.

O conjunto C formado é denominado conjunto interseção de A e B.

Interseção de A e B - diagrama de Venn

Definição: A interseção de dois conjuntos A e B é o conjunto formado pelos elementos que são comuns a A e a B, isto é, pelos elementos que pertencem a A e também pertencem a B.

A ∩ B = {x/x ∈ A e x ∈ B}.

Quando A ∩ B= Ø, os conjuntos A e B são chamados disjuntos.

Propriedades da Interseção

Considerando os conjuntos A, B e C, temos as seguintes propriedades:

A ∩ A = A (idempotente)

A ∩ U = A (elemento neutro)

A ∩ B = B ∩ A (comutativa)

(A ∩ B) ∩ C = A ∩ (B ∩ C) (associativa)

Exemplos:

1) {1,2} ∩ {1,2,3,4} = {1,2}

2) {1,2,3} ∩ {3,4,5,6} = {3}

3) {1,2,3} ∩ {1,2,3} = {1,2,3}

4) {1,2,3} ∩ {4,5,6} = Ø

5) {1,2} ∩ Ø = Ø

Subtração de Conjuntos

Sejam os conjuntos A = {1,2,3,4,5,6,7} e B = {2,4,6,8}.

Podemos determinar um conjunto C formado pelos elementos que pertencem a A, mas que não pertencem a B.

Assim, temos que A ∩ B = {0,2,4}.

Assim,
temos que C = {1,3,5,7}. O conjunto C é chamado diferença A e B.

Definição: A diferença de dois conjuntos A e B é um conjunto dos elementos que pertencem a A mas que não pertencem a B.

A – B= {x/x ∈ A e x ∉ B}

Observação: B – A= {8}. Neste caso, A – B ≠ B – A.

Complementar

Se B ⊂ A, a diferença A – B denomina-se complementar de B em relação a A e indica-se CAb ou !equation! .

CAb = A – B.

Exemplo

Se B = {1,4} e A= {0,1,2,3,4,5}, então CAB = A - B= {0,2,3,5}.

O complementar de B em relação a A é o que falta para B ficar igual a A.

Quantidade de Elementos de Conjuntos

Dados os conjuntos A = {0,1,2,3,4,5} e B = {1,3,5,7,9}, temos que:

n(A) = 6 número de elementos do conjunto A

n(B) = 5 número de elementos do conjunto B

n(A ∪ B) = 8 número de elementos A ∪ B

n(A ∩ B) = 3 número de elementos A ∩ B

De acordo com essas informações, note que:

n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

Exemplo: Em uma universidade são lidos dois jornais A e B. Exatamente 80% dos alunos leem o jornal A e 60% leem o jornal B. Sabendo que todo aluno é leitor de pelo menos
um dos jornais, qual o percentual de alunos que leem ambos os jornais?

O percentual total de alunos é 100%, pois todo aluno lê pelo menos um dos jornais.

n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

100% = 80% + 60% – n(A ∩ B)

            n(A ∩ B) = 40%

O percentual de alunos que leem os dois jornais é de 40%.

Referência

Para saber mais sobre os conceitos básicos de operações de conjuntos, assista ao vídeo KhanAcademy. Disponível em: <https://pt.khanacademy.org/math/ probability/independent-dependent-probability/basic_set_operations/v/ intersection-and-union-of-sets>

Bons Estudos