Conjuntos Numéricos

Conjuntos numéricos

Na matemática, os números são agrupados de acordo com suas características. Esse agrupamento dá origem aos conjuntos numéricos.

Conjunto dos Números Naturais (N)

Ao longo da história, o homem sentiu a necessidade de representar certas situações e de quantificar os objetos. Para tanto, buscou símbolos para atender às suas necessidades, e assim surgiram os números naturais.

N = {0,1,2,3,4,5,6...}

Começando por zero e acrescentando sempre uma unidade, obtemos os elementos do conjunto dos números naturais, indicado pela letra N. O conjunto dos números naturais é infinito, por isso usamos reticências.

Um subconjunto importante de N é o conjunto:

N*{1,2,3,4,5,6,7,8...} = N – {0}

Utiliza-se o asterisco (*) para mostrar que o zero foi excluído.

Os números naturais podem ser representados graficamente. Para isso, usamos uma semirreta sobre a qual marcamos pontos equidistantes a partir da origem.

Representação gráfica dos números naturais

Fonte: Elaborada pela autora

Conjunto dos Números Inteiros (Z)

Com o passar do tempo, a atividade comercial se intensificou, os cálculos começaram a ser utilizados de forma intensa, e assim surgiu a necessidade de novos símbolos para atender às necessidades do momento. Surgiu então o conjunto dos números inteiros, que tinha como objetivo indicar situações como perda e ganho. Os números positivos representavam os ganhos e os números negativos, as perdas.

Então, o conjunto dos números inteiros é composto por zero, números inteiros positivos e negativos.

Z= {...-3, -2,-1,0,1,2,3}

Subconjuntos de Z:

Conjunto dos números naturais é um subconjunto de Z.
Z* = {... -4, -3, -2, -1, 1, 2, 3, 4, ...} conjunto dos números inteiros não nulos.
Z+ = {0,1,2,3,4,5,6, ...} conjunto dos números inteiros não negativos.
Z- = {..., -5, -4, -3, -2, -1, 0} O conjunto dos números inteiros não positivos.

Utiliza-se o asterisco (*) para mostrar que o zero foi excluído: Z*+ e Z*-

Os números inteiros podem ser representados por uma reta numerada.

Representação de Z na reta numérica

Fonte: Elaborada pela autora

Operações entre Números Inteiros

Você sabia?

Um número inteiro é sempre menor que o número inteiro que está à sua direita na reta numérica:

-4 < -1 (-4 é menor que -1)
-2 < 0 (-2 é menor que 0)
3 > -3 (3 é maior que -3)

Adição e Subtração

Na adição e na subtração de números com sinais diferentes: subtrai e conserva o sinal do maior. Exemplos:
– 20 + 3 = – 17 + 48 – 18 = + 30
Números com sinais iguais: soma e conserva o sinal. Exemplos:
– 20 – 5 = – 25 + 18 + 3 = + 21

Multiplicação e Divisão

Para realizar a multiplicação e a divisão entre números inteiros, é preciso fazer a regra dos sinais, em que:

(+) com (+) = +

(–) com (+) = –

(+) com (–) = –

(–) com (–) = +

Exemplos:

+2 · (+5) = + 10
-25 : (+5)= -5
+49 : (-7)= -7
-6 · (-6)= +36

Conjunto dos Números Racionais (Q)

O conjunto dos números racionais surgiu pela necessidade de representar partes de um inteiro e as divisões que obtinham resultados decimais.

Os números que podem ser expressos sob a forma . , sendo a e b números inteiros e b ≠ 0, são denominados números racionais. Exemplos:

. 0,7 4 0,655 2,16666... -25 13%

Representação dos Números Racionais

Todo número racional . pode ser representado por um número decimal, basta dividir o inteiro a pelo inteiro b. Ao representar o número fracionário em decimal podem ocorrer duas situações:

O número decimal tem uma quantidade finita de algarismos, diferentes de zero, ou seja, decimal exata. Exemplo: . = 0,05
O número decimal tem uma quantidade infinita de algarismos que se repetem periodicamente, ou seja, dízima periódica. Exemplo: 1/3 = 0,33333..... = 0,.

A operação inversa também pode ser realizada, ou seja, podemos transformar um número decimal em um número fracionário. Exemplos: 0,45 = . 1,435= .

Quando o decimal é uma dízima periódica, temos de procurar sua geratriz. Exemplos: 0,777...

X = 0,7777... e 10x = 7,777... ⇒ 10x-x = 7 logo x = .

Assista ao vídeo abaixo sobre transformações de decimais em fracionários:

Fonte: Disponível em: https://www.youtube.com/watch?v=oe64-t2d6IM | Acesso em: 6 jan. 2016.

Observação:

Se realizarmos qualquer uma das quatro operações entre dois números racionais quaisquer o resultado também será um número racional.

Representação números racionais

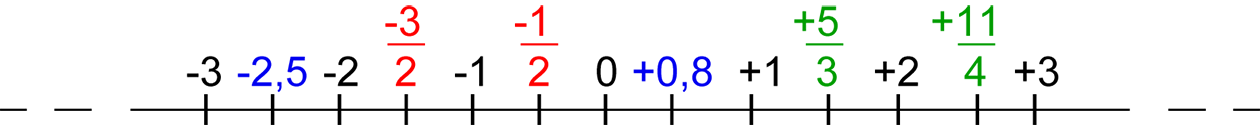
Fonte: http://mundoeducacao.bol.uol.com.br/matematica/comparacao-numeros-racionais.htm

Subconjuntos de Q:

Q₊ conjunto dos racionais não negativos.

Q₋ conjuntos dos números não positivos.

Q* conjunto dos racionais não nulos.

Conjunto dos Números Irracionais (I)

Existem números cuja representação decimal com infinitas casas decimais não é periódica. Eles são denominados números irracionais.

Exemplos:

. = 1,4142135...

. = 1,7320508...

Outro número irracional bem conhecido é o número π = 3,1415926535…

Você sabia?

Se a é irracional e t é racional não nulo, temos que: a+t ; a·t ; . e . são todos irracionais.
Se p é primo e positivo, então é um número irracional.

Conjunto dos Números Reais (R)

O conjunto dos números reais é a junção dos números racionais com os irracionais, ou seja, é o conjunto formado por todos os números com representação decimal, as decimais exatas ou periódicas (números racionais) e as decimais não exatas e não periódicas (números irracionais).

R = Q ∪ I
Conjuntos numéricos

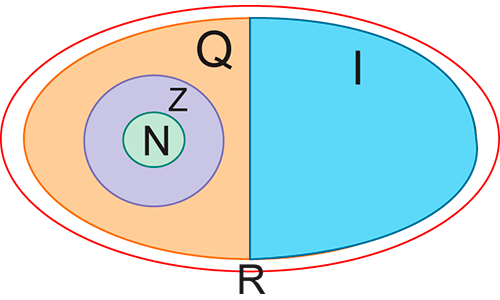
Fonte: Elaborada pela autora

Subconjuntos de R:

R₊ conjunto dos reais não negativos.

R₋ conjunto dos reais não positivos.

R* conjunto dos números não nulos.

Referências

Para saber mais sobre a teoria dos conjuntos, veja o material do Prof. Ulysses Sodré. Disponível em: http://www.uel.br/projetos/matessencial/medio/conjuntos/conjunto.htm | Acesso em: 06/01/2016.

Para ampliar seus conhecimentos sobre conjuntos numéricos, assista ao vídeo disponível em: https://pt.khanacademy.org/math/pre-algebra/fractions-pre-alg/number-sets-pre-alg/v/number-sets-1 | Acesso em: 06/01/2016.

Conjuntos numéricos

Matemática

Conjuntos Numéricos