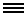When written on a number spiral, primes — represented as darker dots — appear to cluster along certain curves, revealing patterns in the positions of the primes.
If your favorite number is 712, mathematician Andrew Granville will quickly compute that 712 is 2 times 356, 4 times 178, 8 times 89, or 2 times 2 times 2 times 89. "Every number has a unique way of being written down as a product of primes," Granville says. "When we study an object in chemistry, we go to atoms; in biology, we go to DNA. For number theorists, it is prime numbers."
Granville, a professor of mathematics at the University of Montreal, specializes in analytic number theory and properties of prime numbers. On November 18, he delivered the Simons Foundation Lecture "Patterns in the Primes" as part of the foundation's Math and Its Applications lecture series. The foundation began hosting public lectures in 2013 as a way to convene scientists from diverse backgrounds and the interested public. The Math and Its Applications series was launched in 2015 to explore the usefulness of pure mathematics as a tool both to describe empirical reality and to drive human progress.
"The next really great breakthroughs for the progress of humanity often come because brilliant people have read deep mathematical ideas and make startling new connections with them," Granville says.
An example is the mathematics behind the theory of relativity. When, with no particular practical application in mind, Albert Einstein wanted to rework existing ideas in physics, he employed some mathematics that was developed decades earlier to better understand abstract notions in geometry. The resulting work ultimately upended the way we conceive of the universe.
In his lecture, Granville discussed prime numbers as another example of a deep mathematical idea with the potential to transform. A principal reason primes are mysterious, he says, is that they are defined in terms of what they are not: They cannot be divided by any number, aside from one. That makes primes difficult to systematically identify and leads to one of the big questions in studying them: Are there patterns in primes? Ancient Greeks asked such questions more than 2,000 years ago, but we don't have answers to many of those questions even today. Still, Granville says, there have been remarkable breakthroughs recently.
Yitang Zhang of the University of New Hampshire made one of these breakthroughs. Prime numbers become rarer as numbers get bigger. But Zhang wanted to know if larger primes cluster, as smaller primes do, so that there are gaps of length two between them, as with the primes 3 and 5, 5 and 7, and 11 and 13. In 2013, Zhang was able to prove that there are infinitely many such pairs of primes that differ by less than 70 million. Other mathematicians have since pushed the work further, showing there are infinitely many pairs of primes with a maximum gap of 246. Such progress brings mathematicians much closer to solving the famous twin prime conjecture, which states that there are infinitely many pairs of primes that differ by two.
Even though understanding primes can have practical applications —
for data encryption, for example — Granville cautions that we should not place too much
emphasis on practicality in mathematics. "It's a very dangerous question: 'What is this useful for?'" he says. "There is an interesting story to be written
about how practical impracticality
can be."