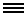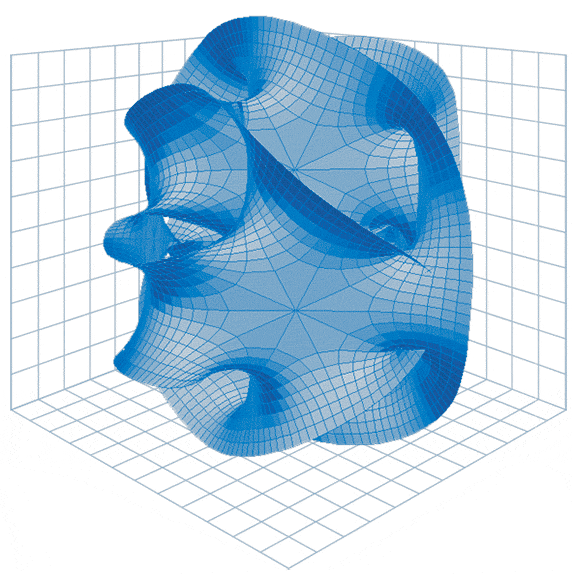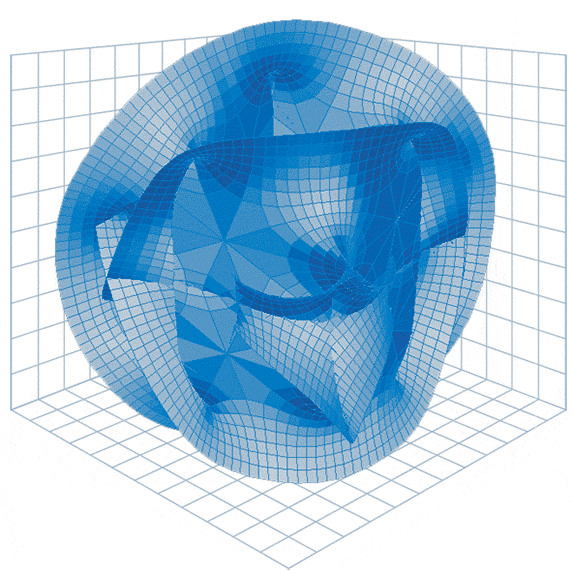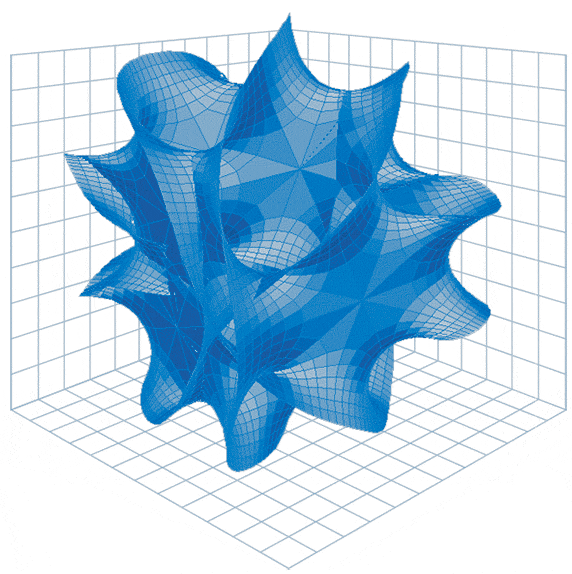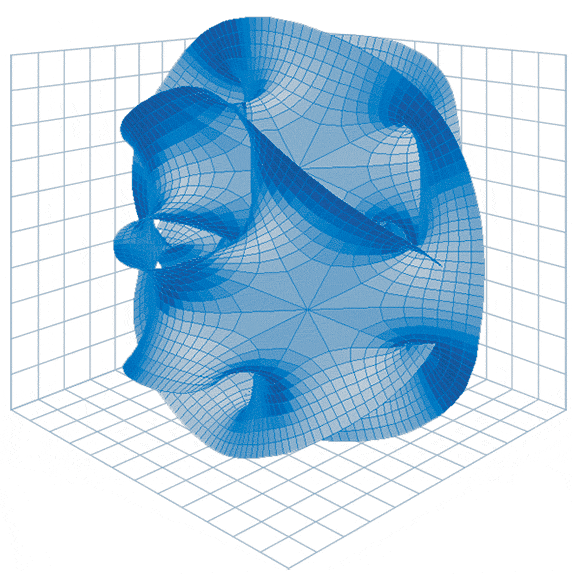
Illustration:
Calabi-Yau manifolds, such as the one shown, are mathematical constructs that string theorists use to add extra dimensions to space-time. These topological
spaces set the framework for mathematicians to begin working on the homological mirror symmetry conjecture, which now includes a broader array of manifolds
beyond Calabi-Yau spaces.
Mathematics could be forgiven for thinking itself a fairy godmother to the other sciences, sprinkling useful theories and theorems into biology, chemistry and physics, enabling them to reach new heights. Sometimes, however, it goes the other way. The Simons Collaboration on Homological Mirror Symmetry, launched in late 2015, works on a field of mathematics inspired by theoretical physics. A successful collaboration would provide mathematicians with a way to translate between seemingly disconnected mathematical realms. The physics inspiration for homological mirror symmetry is string theory, which describes particles as being tiny, vibrating strings. String theory augments our three-dimensional spatial world with an extra six dimensions to make the mathematics of the theory consistent. The extra dimensions are curled up into spaces known as Calabi-Yau manifolds. "Whether this represents the real world is unknown, but there is some fascinating mathematics in there," says Denis Auroux of the University of California, Berkeley, one of the principal investigators of the collaboration.
'Mirror symmetry' here refers to an unexpected correspondence between seemingly unrelated spacetimes: Different Calabi-Yau manifolds described by different
quantum theories turn out to encode the same physics. "All the measurable quantities are the same, even though the models governing the interactions look
completely different," says Tony Pantev of the University of Pennsylvania, director of
the collaboration.
"If you do some kinds of geometric calculations on one and different geometric calculations on the other, you will get the same answer for a reason that is not obvious," says Auroux.
The goal of the Simons collaboration is bold: to prove mirror symmetry in its full generality. Currently, there are three main approaches to homological mirror symmetry that have been developing more or less independently for several years. However, each existing approach can only go so far. "They've gotten quite a lot of momentum," Pantev says, "but it's clear that we have to combine the approaches to get the full solution." The collaboration brings together prominent researchers in each branch to see where they can combine their ideas. "We've gotten enough cross-pollination between these approaches in recent years to understand that we can now really work on the merger," says Pantev.
In 1994, Maxim Kontsevich, who has appointments at both the Institut des Hautes Études Scientifiques in France and the University of Miami, formulated the homological mirror symmetry conjecture, taking mirror symmetry beyond its origin in physics into the world of mathematics. The conjecture he formulated relates objects in two different mathematical worlds, says Pantev. "One is the world of complex geometry, which is fairly robust and rigid and very complicated, the other is the world of symplectic topology, which is kind of flabby and has a lot of wiggle space in it, and is hard to pin down." The conjecture is that every symplectic manifold has a mirror pair in the complex geometry world and that an invariant of the symplectic manifold, known as the Fukaya category, is the same as an invariant called the derived category of its mirror space.
Pantev describes homological mirror symmetry as a dictionary between the symplectic geometry world and the complex geometry world. "There are many
questions in both mathematical universes that this dictionary relates that become really accessible and easy once you pipe them through the dictionary," he
says. "But first you need to establish the dictionary," or, in other words, prove the homological mirror
symmetry conjecture.
In addition to Auroux, Kontsevich and Pantev, principal investigators include Mohammed Abouzaid of Columbia University, Ron Donagi of the University of Pennsylvania, Kenji Fukaya of the Simons Center for Geometry and Physics, Ludmil Katzarkov of the University of Miami and the University of Vienna, Bong Lian of Brandeis University and Shing-Tung Yau of Harvard University. The project launched in November with an inaugural conference at the University of Pennsylvania, and in the coming years it will host several workshops and conferences per year. A successful proof of homological mirror symmetry would have a large, immediate effect on mathematics. First, it has the potential to make difficult questions in symplectic geometry or complex geometry more tractable by allowing researchers to translate the questions into the other realm and try to solve them there.
A proof of homological mirror symmetry would have surprising and paradigm-changing effects in other areas as well. The Langlands program is another long-standing avenue of research in mathematics that explores surprising relationships between mathematical objects from different realms. One part of the Langlands program, geometric Langlands, is "a special kind of mirror symmetry that descends from electric-magnetic duality in four dimensions," says Edward Witten of the Institute for Advanced Study in Princeton. Thus, a proof of homological mirror symmetry would imply a proof of the geometric Langlands correspondence, a huge breakthrough in the field.
Unlike general relativity, for which the necessary mathematics, Riemannian geometry, had already been developed when Albert Einstein needed it,
mathematical research in mirror symmetry was precipitated by physicists. "It's fun because in pure math, usually people work on questions that are very old
and very internal. Somehow the answer always comes from within mathematics," Auroux says. "This is a field where physicists came up with this prediction,
and we're still
playing with it."